基础架构 1、数组与函数的关系 数组与函数并无本质区别,均是一种映射的形式。变量函数,指针数组。
数组:展开的函数,关键在于指针变化,查询时间快。
函数:压缩的数组,关键在于值传递,用INDEX来定位,所用空间小。
算法中的时空互换逻辑,时间复杂度与空间复杂度可以一定程度互换。
2、C++的编程逻辑 面向过程:自顶向下的编程,性能高,但需要处理实现性能的每一个细节,难以复用、扩展。
面向对象:抽象化事物,建立模型。
函数式编程:强调将计算过程分解成可复用的函数,MAP方法。
1 auto add = [](int a,int b) -> int {return a+b};
泛型编程:STL,编写完全一般化并可重复使用的算法,其效率与针对某特定数据类型而设计的算法相同;泛型:在多种数据类型上皆可操作;将算法与数据结构完全分离。
1 2 3 template <typename T ,typename U >auto add(T a, U , b) -> decltype (a+b)return a + b
3、程序执行的底层 C源码—编译—》对象文件—链接—》可执行程序 编译时:语法检查,一个源码生成一个目标文件
对象文件:存储各种各样定义
链接:需将所有对象文件定义捏合在一起
定义:函数具体的实现过程在这(有地址空间的为定义)
声明:说有这样一个东西(无地址空间为声明),作用于编译阶段用于语法检查,在调用函数时做语法检查,仅包含函数传入参数与返回值,并不关心函数内部
nm -C main.O
查看main.O该对象文件内容,main.O中printf由系统库实现,add由自定库实现
为何要分开定义与声明?
.h头文件—》放置声明 源文件—》放置定义 把定义放在头文件往往会产生bug
apt-get install vim.deb; ctrl +t 打开中断
凡是未定义(undefined)、冲突(duplicate:符号定义有2个)的错误—》一般是链接阶段的错误;
4、google测试框架 要实现第三方模块功能的引入—》引入头文件 .h
其定义压缩在一起生成了库文件:静态链接库: .lib
IDE:集成开发环境=文本(vim,gcc) + 编译(g++) + 调试(gdb,lldb)
添加谷歌测试框架 使用make命令
一般未定义、重复定义的错误:一般均出现在链接阶段的错误。
而找不到头文件的错误,一般出现在预编译阶段,需要添加上头文件的编译路径。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 using namespace std ;int add (int a, int b) return a + b } TEST(test, add1){ EXPECT_EQ(add(3 ,4 ),7 ); EXPECT_NQ(add(3 ,4 ),6 ); EXPECT_LT(add(3 ,4 ),8 ); EXPECT_LE(add(3 ,4 ),7 ); EXPECT_GT(add(3 ,4 ),6 ); EXPECT_GE(add(3 ,4 ),7 ); } TEST(test, add2){ EXPECT_EQ(add(3 ,4 ),7 ); EXPECT_NQ(add(3 ,4 ),7 ); EXPECT_LT(add(3 ,4 ),7 ); EXPECT_LE(add(3 ,4 ),7 ); EXPECT_GT(add(3 ,4 ),7 ); EXPECT_GE(add(3 ,4 ),7 ); }
谷歌测试框架中Run_All:1、能够输出彩色字体;2、能够动态地获取知道有多少个测试用例
使用printf输出彩色信息 使用printf输出信息之前,可以在printf添加配置参数,调整输出的字体颜色。以\033[开头,以m结尾
1 2 printf ("\033[1;33;41madd(3,4) = %d\n" ,add(3 ,4 ));printf ("hello world\n" );
两行的内容均会改变颜色,因为底层的信息决定了显示的颜色,而终端的程序就是** 用来显示底层信息**的。我们上述的修改是修改了自己配置颜色信息的部分,因此Terminal看到了设置背景色、前景色之后时,之后打印均按照该信息进行,直到后续碰到谷歌框架配置颜色信息的代码时,才按照该框架的配置来显示颜色。
在该配置中0为重置所有属性,故可用下列代码确保仅一行输出改变颜色,\033[0m
1 2 printf ("\033[1;33;41madd(3,4) = %d\n\033[0m" ,add(3 ,4 ));printf ("hello world\n" );
实现调试信息log日志打印功能 在大型工程中同样的调试信息输出代码很常见,故难以判断调试信息在哪输出,因此需要能输出功能更丰富的输出调试信息。
预处理命令:宏定义#define :1、定义符号常量;2、定义傻瓜表达式;3、定义代码段
宏做的事情就是最基本的替换,发生在预处理阶段
*C源码–预处理–》待编译 + 代码 –编译 –目标文件–链接–》可执行文件*
g++ -E :单独执行预处理阶段
最终决定程序功能的并不是C源码,而是待编译源码。因此需要经过预处理阶段之后补充代码之后,才能够正确的实现功能。
#define:宏定义,只做基础的替换,而不做语法检查,且在编译器的视角中,宏定义一定要是一行代码。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 #define s(a,b) a*b s(int , p) = &n; #这句代码是正确的,因为define并不检查语法,而是只做基础替换,替换后变为: int *p = &n; s(3 +6 ,4 ); #预处理后成为3 +6 *4 ;因此输出为27 ,而不是4 *9 =36 #define P(a){\ printf ("%d\n" , d);\} #利用反斜杠让编译器认为上面的宏定义其实是一行代码 #预定义的宏 #_DATE_ 日期 #_TIME_ 时间 #_LINE_ 行号 #_FILE_ 文件名 #_func_ 函数名/非标准 #_FUNC_ 函数名/标准 #_PRETTY_FUNCTION_ 更详细的函数信息 这些预定义的宏信息可用于检查版本,同样也可用于调试信息log 日志打印 #define log(msg) {\ printf ("[%s : %s : %d] %s\n" , __FILE__, __func__, __LINE__, msg) ;\ } 故通过log 能够打印出调试信息从而进行分析 如何根据上述地修改下,实现任意参数的宏,变参函数、变参宏 #define log(frm, args...) {\ printf ("[%s : %s : %d] %s\n" , __FILE__, __func__, __LINE__, msg) ;\ printf (frm,##args);\ printf ("\n" );\ } 这样就实现了一个外在表现像是printf 函数的宏,其输出信息会更多许多
#include:将后面文件内容原封不动地拷被至该位置,故待编译源码才能完整地反映功能。
#const:分配空间
预处理命令-条件编译 如何确保在发布版中没有日志信息,即需要用简单的方式对日志信息创建开关,必须以#endif 结尾
预处理的条件编译只有一个作用:做代码剪裁,使用该命令决定留下哪些代码
实现EXCEPT系列封装 将谷歌测试框架的头文件换成自己的头文件,并编写自己头文件程序完成同样代码的编译;
1、实现TEST方法;2、实现未卜先知函数RUN_ALL_TEST;3、实现相等、不等、小于等判断方法,可判断不是由函数封装出来的,而是用宏进行封装;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 #ifndef _MYTEST_H #define _MYTEST_H #define EXPECT_EQ(a,b){\ if (!((a) == (b)){\ print ("error\n" );}} #define EXPECT_NE(a,b){\ if (!((a) != (b)){\ print ("error\n" );}} #define EXPECT_EQ(a,b){\ if (!((a) < (b)){\ print ("error\n" );}} 其实此处代码可以进行复用,来使代码变得简洁,用宏能做的基础替换来进行复用。 #define EXPECT(a, comp, b){\ if (!((a) comp (b)){\ print ("error\n" );} } #define EXPECT_EQ(a, b) EXPECT(a, == ,b) #define EXPECT_NE(a, b) EXPECT(a, != ,b) #define EXPECT_LT(a, b) EXPECT(a, < ,b) #define EXPECT_LE(a, b) EXPECT(a, <= ,b) #define EXPECT_GT(a, b) EXPECT(a, > ,b) #define EXPECT_GE(a, b) EXPECT(a, >= ,b) TEST应当是宏,在预编译后应当展开为函数的头部信息 #define TEST(a, b) void a##_##b() 如何实现RUN_ALL_TEST未卜先知函数 如何确保将测试用例函数信息写入存储区:注册函数 #define TEST(a, b)\ void a##_##b();\__attribute__((constructor))\ void reg_##a##_##b(){\ add_test_func(a##_##b, #a'.' #b);\ return ;\ } struct{ void (*func)(); const char *func_name; } func_arr[100 ]; int_func_cont = 0 ; void add_test_func(void (*func)(), const *name){ func_arr[func_cnt].func =func; func_Arr[func_cnt].func_name = name; func_cnt += 1 ; return ; } int RUN_ALLO_TEST{\ for (int i = 0 ; i < func_cntr; i++){ print ("[ RUN ]%S\n" ,func_arr[i]->name); func_arr[i].func(); } return 0 ; } #endif
5、简单算法 二分查找:在一个有序数组中查找一个数据是否存在;二分函数:二分查找如何处理浮点型数据,连续函数;二分答案
本质:二分查找解决的问题:求解单调函数F(x),函数与数组关系,其实和有序数组查找值一样的方法;
应用特点:给出X很好求,但F(X)并不好求。对于F(X) = 2X,这种正反均好求时,用不着二分查找;而对于在数组中,给出数组下标容易得出值,但给出值查找下标较为困难。
简单版快速排序: 核心:partation方法,分区方法,
头部指针、尾部指针:1、先尾部指针,找一个小于基准值放前面;2、再头部指针:找一个大于基准值的放后面;3、头尾指针依次进行交替,直至指针指向同一空位置;
写一个用于测试快速排序的程序:TEST.H
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 #define TEST(func, arr, l, r){ int *temp = (int *)malloc (sizeof (int ) * n); for (int i = 0 ; i <n; i++) temp[i] = arr[i]; func(temp, 0 ,n-1 ); if (check(temp, 0 , n-1 )){ print ("[ OK ]%s\n" , #func); }else { print ("[ FAILED ]%s\n" , #func); } } int check (int *arr, int l, int r) for (int i = l + 1 ; i <= r; i++){ if (arr[i] < arr[i-1 ]) return 0 ; } return 1 ; } int *getRandData (int n) int *arr = (int *)malloc (sizeof (int ) * n); for (int i = 0 ; i < n; i++) arr[i] = rand() % n; return arr; } int main{ }
version1 partation:选择待排序区间的第一个元素作为基准值,将小于基准值的元素放在前面,大于基准值的元素放在后面,前后指针重合时,再分别对前后两部分进行快速排序的操作。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 void quick_sort_v1 (int *arr_, int l , int r) if (l >= r) return ; int x = 1 ; y = r; z = arr[]; while (x < y){ while (x < y && arr[y] >= z) --y; if (x < y) arr[x++] = arr[y]; while (x < y && arr[x] <= z) ++x; if (x < y) arr[y--] = arr[x]; } arr[x] = z; quick_sort_v1(arr, l, x - 1 ); quick_sort_va(arr, x + 1 , r); return ; }
算法工程师平时考虑的是时间复杂度吗?
大环境下的共识:你和你身边的同事都是算法工程师,因此nlogn时间复杂度算法都能想到,关键在于在实现时代码实现的细节;
version2:单边递归法 当本层的快速排序做完partation操作时,会分别对左右两边进行递归操作,因此相当于一个二叉树的结构;
单边递归法核心思想:作为一个主管,在要被优化掉之前,做下一层的活。当前的version1函数,partation做完之后等着左右两边,可以让左半边继续递归,但右半边交给当前层程序进行执行。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 void quick_sort_v2 (int *arr_, int l , int r) while (l < r){ int x = l ; y = r; z = arr[l]; while (x < y){ while (x < y && arr[y] >= z) --y; if (x < y) arr[x++] = arr[y]; while (x < y && arr[x] <= z) ++x; if (x < y) arr[y--] = arr[x]; } arr[x] = z; quick_sort_v2(arr, l, x - 1 ); l = x + 1 ; } return ; }
version3:无监督优化 凡是判断坐标范围超界的判断:均为监督项,无监督优化:将监督项干掉;
先以插入排序来举例子:
插入排序思想:将无序序列分成两部分,前半部分为已排序区,后半部分为未排序区,每次从未排序区的头部选择一个元素,插入至已排序区中。
1 2 3 4 5 6 7 8 9 10 void insert_sort_v1 (int *arr, int l, int r) for (int i = l + 1 ; i <= r; i++){ int j = i; while (j > 0 && arr[j] < arr[j - 1 ]){ swap(arr[j], arr[j-1 ]); --j; } } return ; }
无监督思想:为何需要监督项,确保指针访问不越界,那么如何才能去掉这个监督项看上述while(j > 0 && arr[j] < arr[j - 1]),只有当前插入的元素,是当前已排序区间的最小值,才会越界;因此,先做一个预处理,将该全局范围内的最小值先放置第一位,则不可能发生这种越界操作,则不再需要插入排序中的监督项。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 void insert_sort_v2 (int *arr, int l, int r) int ind = l; for (int i = l + 1 ; i <= r; i++){ if (arr[ind] > arr[i]) ind = i; } while (ind > l){ swap(arr[ind], arr[ind -1 ]); --ind; } for (int i = l + 1 ; i <= r; i++){ int j = i; while (j > 0 && arr[j] < arr[j - 1 ]){ swap(arr[j], arr[j-1 ]); --j; } } return ; }
那么如何实现无监督的快速排序呢?快速排序中的partation过程,小于基准值放在前,大于的放在后;逻辑上讲,确定基准值后,其前后元素的数量就已经定了,由于基准值前后的位置数量是固定的,则有前一个值往后移、则必然后后面一个元素向前移。
故可以头尾指针同时向中间走,且两者同时进行交换,这样就能去掉快速排序过程中其所谓的监督项了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 void quick_sort_v3 (int *arr_, int l , int r) while (l < r){ int x = 1 , y = r, z = arr[l]; do { while (arr[x] < z) ++x; while (arr[y] > z) --y; if (x <= y){ swap(arr[x], arr[y]); ++x, --y; } }while (x <= y); quick_sort_v3(arr, l, y); l = x ; } return ; }
无监督的算法优化思维是一种非常重要的代码优化思维。
version4:基准值选择优化 核心思维:快速排序时间复杂度,T(n) = n * h,其中h为递归二叉树的树高,而递归二叉树最多为n个节点,logn < h < n;则nlogn < T(n) < n**2
如何让快排的时间复杂度稳定在nlogn:控制二叉树树高,即每一次区分左右树时,尽量让左右两边平分,即基准值能平分数组。
方法一:三点取中法,在头指针l,尾指针r,中间元素指针m,三者指向的值之间,选取中位的那个数值作为基准值。
6、虚函数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 class A { public : void say () cout << "this is Class A" << endl ; } }; class B :public A { public : void say () cout << "this is class B" << endl ; } }; int main () B b; A &a = b; A *c = &b; b.say(); a.say(); c->say(); return 0 ; } class C { public : virtual void say () cout << "this is Class A" << endl ; } }; class D :public C { public : void say () cout << "this is class B" << endl ; } }; int main () B b; A &a = b; A *c = &b; b.say(); a.say(); c->say(); return 0 ; }
为什么虚函数可以跟着对象走: 任何一个对象都会占据一片存储空间,当对象中存在虚函数时,其底层存储区域中的第一个位置会记录一个地址;该地址指向一张虚函数的表vtable,表中每一项都存储的是虚函数。
因此虚函数是跟着对象走的,不管是何种类型的对象,都会指向了虚函数表,从而调用了当前对象所绑定的虚函数方法。
假设虚函数类型为T类型,则虚函数表首地址为T* 类型, 则存储T*类型数据区的数据为T**类型。因此可用C语言中指针来提取虚函数。但若用此方法来提取带参数的虚函数时,可能会导致参数混乱。
this指针 原因是:在成员方法中的特殊变量:this指针,在成员方法中,看着是一个参数,实则会添加一个隐藏参数:this指针。因此两个参数:一个是this指针指向的地址,一个才是真正的传递参数。
this指针其实是一个变量,是成员方法的隐藏参数。
C++基础 基本语法
对象 - 对象具有状态和行为。例如:一只狗的状态 - 颜色、名称、品种,行为 - 摇动、叫唤、吃。对象是类的实例。类 - 类可以定义为描述对象行为/状态的模板/蓝图。方法 - 从基本上说,一个方法表示一种行为。一个类可以包含多个方法。可以在方法中写入逻辑、操作数据以及执行所有的动作。即时变量 - 每个对象都有其独特的即时变量。对象的状态是由这些即时变量的值创建的。
数据类型
布尔型
bool
字符型
char
整型
int
浮点型
float
双浮点型
double
无类型
void
宽字符型
wchar_t
endl ,这将在每一行后插入一个换行符,<< 运算符用于向屏幕传多个值
可以使用 typedef 为一个已有的类型取一个新的名字。下面是使用 typedef 定义一个新类型的语法:
现在,下面的声明是完全合法的,它创建了一个整型变量 distance:
1 2 typedef int feet;feet distance;
枚举类型 枚举类型(enumeration)是C++中的一种派生数据类型,它是由用户定义的若干枚举常量的集合。建枚举,需要使用关键字 enum 。枚举类型的一般形式为:
1 2 3 4 5 6 7 8 9 10 11 enum 枚举名{ 标识符[=整型常数], 标识符[=整型常数], ... 标识符[=整型常数] } 枚举变量; enum color { red, green, blue } c;c = blue;
变量类型 变量其实只不过是程序可操作的存储区的名称。C++ 中每个变量都有指定的类型,类型决定了变量存储的大小和布局,该范围内的值都可以存储在内存中,运算符可应用于变量上。
bool
存储值 true 或 false。
char
通常是一个字符(八位)。这是一个整数类型。
int
对机器而言,整数的最自然的大小。
float
单精度浮点值。单精度是这样的格式,1位符号,8位指数,23位小数。
double
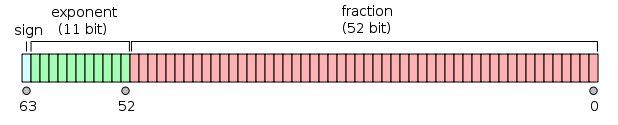
双精度浮点值。双精度是1位符号,11位指数,52位小数。
void
表示类型的缺失。
wchar_t
宽字符类型。
变量定义就是告诉编译器在何处创建变量的存储,以及如何创建变量的存储。变量定义指定一个数据类型,并包含了该类型的一个或多个变量的列表,
变量声明向编译器保证变量以给定的类型和名称存在,这样编译器在不需要知道变量完整细节的情况下也能继续进一步的编译。变量声明只在编译时有它的意义,在程序连接时编译器需要实际的变量声明。
当您使用多个文件且只在其中一个文件中定义变量时(定义变量的文件在程序连接时是可用的),变量声明就显得非常有用。您可以使用 extern 关键字在任何地方声明一个变量。虽然您可以在 C++ 程序中多次声明一个变量,但变量只能在某个文件、函数或代码块中被定义一次。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 #include <iostream> using namespace std ; extern int a, b;extern int c;extern float f; int main () int a, b; int c; float f; a = 10 ; b = 20 ; c = a + b; cout << c << endl ; f = 70.0 /3.0 ; cout << f << endl ; return 0 ; }
同样的,在函数声明时,提供一个函数名,而函数的实际定义则可以在任何地方进行。例如
1 2 3 4 5 6 7 8 9 10 11 12 13 14 int func () int main () int i = func(); } int func () return 0 ; }
C++ 中有两种类型的表达式:
左值(lvalue): 指向内存位置、的表达式被称为左值(lvalue)表达式。左值可以出现在赋值号的左边或右边。右值(rvalue): 术语右值(rvalue)指的是存储在内存中某些地址的数值。右值是不能对其进行赋值的表达式,也就是说,右值可以出现在赋值号的右边,但不能出现在赋值号的左边。
变量是左值,因此可以出现在赋值号的左边。数值型的字面值是右值,因此不能被赋值,不能出现在赋值号的左边。下面是一个有效的语句:
变量作用域 作用域是程序的一个区域,一般来说有三个地方可以定义变量:
在函数或一个代码块内部声明的变量,称为局部变量。
在函数参数的定义中声明的变量,称为形式参数。
在所有函数外部声明的变量,称为全局变量。
在函数或一个代码块内部声明的变量,称为局部变量。它们只能被函数内部或者代码块内部的语句使用。
在所有函数外部定义的变量(通常是在程序的头部),称为全局变量。全局变量的值在程序的整个生命周期内都是有效的。
在程序中,局部变量和全局变量的名称可以相同,但是在函数内,局部变量的值会覆盖全局变量的值。
字面量 常量是固定值,在程序执行期间不会改变。这些固定的值,又叫做字面量 。
常量可以是任何的基本数据类型,可分为整型数字、浮点数字、字符、字符串和布尔值。
在 C++ 中,有两种简单的定义常量的方式:
使用 #define 预处理器。
使用 const 关键字。
修饰符类型 C++ 允许在 char、int 和 double 数据类型前放置修饰符。修饰符用于改变基本类型的含义,所以它更能满足各种情境的需求。
修饰符 signed、unsigned、long 和 short 可应用于整型,signed 和 unsigned 可应用于字符型,long 可应用于双精度型。
修饰符 signed 和 unsigned 也可以作为 long 或 short 修饰符的前缀。例如:unsigned long int 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 #include <iostream> using namespace std ; int main () short int i; short unsigned int j; j = 50000 ; i = j; cout << i << " " << j; return 0 ; }
存储类 存储类定义 C++ 程序中变量/函数的范围(可见性)和生命周期。这些说明符放置在它们所修饰的类型之前。下面列出 C++ 程序中可用的存储类:
auto
register
static
extern
mutable
thread_local (C++11)
auto 存储类 自 C++ 11 以来,auto 关键字用于两种情况:声明变量时根据初始化表达式自动推断该变量的类型、声明函数时函数返回值的占位符。
register 存储类 register 存储类用于定义存储在寄存器中而不是 RAM 中的局部变量。这意味着变量的最大尺寸等于寄存器的大小(通常是一个词),且不能对它应用一元的 ‘&’ 运算符(因为它没有内存位置)
寄存器只用于需要快速访问的变量,比如计数器。
static 存储类 static 存储类指示编译器在程序的生命周期内保持局部变量的存在,而不需要在每次它进入和离开作用域时进行创建和销毁。因此,使用 static 修饰局部变量可以在函数调用之间保持局部变量的值。
static 修饰符也可以应用于全局变量。当 static 修饰全局变量时,会使变量的作用域限制在声明它的文件内。在 C++ 中,当 static 用在类数据成员上时,会导致仅有一个该成员的副本被类的所有对象共享。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 #include <iostream> void func (void ) static int count = 10 ; int main () while (count--) { func(); } return 0 ; } void func ( void ) static int i = 5 ; i++; std ::cout << "变量 i 为 " << i ; std ::cout << " , 变量 count 为 " << count << std ::endl ; }
extern 存储类 extern 存储类用于提供一个全局变量的引用,全局变量对所有的程序文件都是可见的。当您使用 ‘extern’ 时,对于无法初始化的变量,会把变量名指向一个之前定义过的存储位置。
当您有多个文件且定义了一个可以在其他文件中使用的全局变量或函数时,可以在其他文件中使用 extern 来得到已定义的变量或函数的引用。可以这么理解,extern 是用来在另一个文件中声明一个全局变量或函数。
extern 修饰符通常用于当有两个或多个文件共享相同的全局变量或函数的时候,如下所示:
第一个文件:main.cpp
在这里,第二个文件中的 extern 关键字用于声明已经在第一个文件 main.cpp 中定义的 count。现在 ,编译这两个文件,如下所示
mutable 存储类 mutable 说明符仅适用于类的对象,这将在本教程的最后进行讲解。它允许对象的成员替代常量。也就是说,mutable 成员可以通过 const 成员函数修改。
thread_local 存储类 使用 thread_local 说明符声明的变量仅可在它在其上创建的线程上访问。 变量在创建线程时创建,并在销毁线程时销毁。 每个线程都有其自己的变量副本。
thread_local 说明符可以与 static 或 extern 合并。可以将 thread_local 仅应用于数据声明和定义,thread_local 不能用于函数声明或定义。以下演示了可以被声明为 thread_local 的变量:
1 2 3 4 5 6 7 8 9 10 11 thread_local int x; class X { static thread_local std ::string s; }; static thread_local std ::string X::s; void foo () thread_local std ::vector <int > v; }
运算符
算术运算符 + - * / % ++ –
关系运算符 == != > < >= <=
逻辑运算符 && || !
位运算符
& 如果同时存在于两个操作数中,二进制 AND 运算符复制一位到结果中。 (A & B) 将得到 12,即为 0000 1100
|
如果存在于任一操作数中,二进制 OR 运算符复制一位到结果中。
(A | B) 将得到 61,即为 0011 1101
^
如果存在于其中一个操作数中但不同时存在于两个操作数中,二进制异或运算符复制一位到结果中。
(A ^ B) 将得到 49,即为 0011 0001
~
二进制补码运算符是一元运算符,具有”翻转”位效果,即0变成1,1变成0。
(~A ) 将得到 -61,即为 1100 0011,一个有符号二进制数的补码形式。
<<
二进制左移运算符。左操作数的值向左移动右操作数指定的位数。
A << 2 将得到 240,即为 1111 0000
>>
二进制右移运算符。左操作数的值向右移动右操作数指定的位数。
A >> 2 将得到 15,即为 0000 1111
赋值运算符
=
简单的赋值运算符,把右边操作数的值赋给左边操作数
C = A + B 将把 A + B 的值赋给 C
+=
加且赋值运算符,把右边操作数加上左边操作数的结果赋值给左边操作数
C += A 相当于 C = C + A
-=
减且赋值运算符,把左边操作数减去右边操作数的结果赋值给左边操作数
C -= A 相当于 C = C - A
*=
乘且赋值运算符,把右边操作数乘以左边操作数的结果赋值给左边操作数
C *= A 相当于 C = C * A
/=
除且赋值运算符,把左边操作数除以右边操作数的结果赋值给左边操作数
C /= A 相当于 C = C / A
%=
求模且赋值运算符,求两个操作数的模赋值给左边操作数
C %= A 相当于 C = C % A
<<=
左移且赋值运算符
C <<= 2 等同于 C = C << 2
>>=
右移且赋值运算符
C >>= 2 等同于 C = C >> 2
&=
按位与且赋值运算符
C &= 2 等同于 C = C & 2
^=
按位异或且赋值运算符
C ^= 2 等同于 C = C ^ 2
|=
按位或且赋值运算符
C |= 2 等同于 C = C | 2
杂项运算符
sizeof
sizeof 运算符 返回变量的大小。例如,sizeof(a) 将返回 4,其中 a 是整数。
Condition ? X : Y
条件运算符 。如果 Condition 为真 ? 则值为 X : 否则值为 Y。
,
逗号运算符 会顺序执行一系列运算。整个逗号表达式的值是以逗号分隔的列表中的最后一个表达式的值。
.(点)和 ->(箭头)
成员运算符 用于引用类、结构和共用体的成员。
Cast
强制转换运算符 把一种数据类型转换为另一种数据类型。例如,int(2.2000) 将返回 2。
&
指针运算符 & 返回变量的地址。例如 &a; 将给出变量的实际地址。
*
指针运算符 * 指向一个变量。例如,*var; 将指向变量 var。
循环 循环控制语句更改执行的正常序列。当执行离开一个范围时,所有在该范围中创建的自动对象都会被销毁。
控制语句
描述
break 语句 终止 loop 或 switch 语句,程序流将继续执行紧接着 loop 或 switch 的下一条语句。
continue 语句 引起循环跳过主体的剩余部分,立即重新开始测试条件。
goto 语句 将控制转移到被标记的语句。但是不建议在程序中使用 goto 语句。
函数 调用函数 创建 C++ 函数时,会定义函数做什么,然后通过调用函数来完成已定义的任务。
当程序调用函数时,程序控制权会转移给被调用的函数。被调用的函数执行已定义的任务,当函数的返回语句被执行时,或到达函数的结束括号时,会把程序控制权交还给主程序。
调用函数时,传递所需参数,如果函数返回一个值,则可以存储返回值。例如:
函数参数 如果函数要使用参数,则必须声明接受参数值的变量。这些变量称为函数的形式参数 。
形式参数就像函数内的其他局部变量,在进入函数时被创建,退出函数时被销毁。
当调用函数时,有三种向函数传递参数的方式:
调用类型
描述
传值调用 该方法把参数的实际值赋值给函数的形式参数。在这种情况下,修改函数内的形式参数对实际参数没有影响。
指针调用 该方法把参数的地址赋值给形式参数。在函数内,该地址用于访问调用中要用到的实际参数。这意味着,修改形式参数会影响实际参数。
引用调用 该方法把参数的引用赋值给形式参数。在函数内,该引用用于访问调用中要用到的实际参数。这意味着,修改形式参数会影响实际参数。
默认情况下,C++ 使用传值调用来传递参数。一般来说,这意味着函数内的代码不能改变用于调用函数的参数。之前提到的实例,调用 max() 函数时,使用了相同的方法。
向函数传递参数的引用调用 方法,把引用的地址复制给形式参数。在函数内,该引用用于访问调用中要用到的实际参数。这意味着,修改形式参数会影响实际参数。
按引用传递值,参数引用被传递给函数,就像传递其他值给函数一样。因此相应地,在下面的函数 swap() 中,您需要声明函数参数为引用类型,该函数用于交换参数所指向的两个整数变量的值。
1 2 3 4 5 6 7 8 9 10 void swap (int &x, int &y) int temp; temp = x; x = y; y = temp; return ; }
引用的一个重要作用就是作为函数的参数。以前的C语言中函数参数传递是值传递,如果有大块数据作为参数传递的时候,采用的方案往往是指针,因为 这样可以避免将整块数据全部压栈,可以提高程序的效率。但是现在(C++中)又增加了一种同样有效率的选择(在某些特殊情况下又是必须的选择),就是引 用。
如果既要利用引用提高程序的效率,又要保护传递给函数的数据不在函数中被改变,就应使用常引用。常引用声明方式:const 类型标识符 &引用名=目标变量名;用这种方式声明的引用,不能通过引用对目标变量的值进行修改,从而使引用的目标成为const,达到了引用的安全性。
要以引用返回函数值,则函数定义时要按以下格式:
类型标识符 &函数名(形参列表及类型说明)
说明:(1)以引用返回函数值,定义函数时需要在函数名前加&
(2)用引用返回一个函数值的最大好处是,在内存中不产生被返回值的副本。
数组 多维数组:
1 2 3 4 5 6 7 8 9 10 type name[size1][size2]...[sizeN]; int threedim[5 ][10 ][4 ];int a[3 ][4 ] = { {0 , 1 , 2 , 3 } , {4 , 5 , 6 , 7 } , {8 , 9 , 10 , 11 } };
指向数组的指针:runoobAarray 是一个指向 &runoobAarray[0] 的指针,即数组 runoobAarray 的第一个元素的地址。一旦您把第一个元素的地址存储在 p 中,您就可以使用 p、 (p+1)、*(p+2) 等来访问数组元素。
C++ 中您可以通过指定不带索引的数组名来传递一个指向数组的指针。C++ 传数组给一个函数,数组类型自动转换为指针类型,因而传的实际是地址。
如果您想要在函数中传递一个一维数组作为参数,您必须以下面三种方式来声明函数形式参数,这三种声明方式的结果是一样的,因为每种方式都会告诉编译器将要接收一个整型指针。同样地,您也可以传递一个多维数组作为形式参数。
1 2 3 4 5 6 void myFunction (int *param) . . . }
C++ 不允许返回一个完整的数组作为函数的参数。但是,您可以通过指定不带索引的数组名来返回一个指向数组的指针。
如果您想要从函数返回一个一维数组,您必须声明一个返回指针的函数,如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 int * myFunction () . . . } #include <iostream> #include <cstdlib> #include <ctime> using namespace std ; int * getRandom ( ) static int r[10 ]; srand( (unsigned )time( NULL ) ); for (int i = 0 ; i < 10 ; ++i) { r[i] = rand(); cout << r[i] << endl ; } return r; } int main () int *p; p = getRandom(); for ( int i = 0 ; i < 10 ; i++ ) { cout << "*(p + " << i << ") : " ; cout << *(p + i) << endl ; } return 0 ; }
引用 引用很容易与指针混淆,它们之间有三个主要的不同:
不存在空引用。引用必须连接到一块合法的内存。
一旦引用被初始化为一个对象,就不能被指向到另一个对象。指针可以在任何时候指向到另一个对象。
引用必须在创建时被初始化。指针可以在任何时间被初始化。
试想变量名称是变量附属在内存位置中的标签,您可以把引用当成是变量附属在内存位置中的第二个标签。因此,您可以通过原始变量名称或引用来访问变量的内容。例如:
1 2 int & r = i;double & s = d;
在这些声明中,& 读作引用 。因此,第一个声明可以读作 “r 是一个初始化为 i 的整型引用”,第二个声明可以读作 “s 是一个初始化为 d 的 double 型引用”。下面的实例使用了 int 和 double 引用:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 #include <iostream> using namespace std ; int main () int i; double d; int & r = i; double & s = d; i = 5 ; cout << "Value of i : " << i << endl ; cout << "Value of i reference : " << r << endl ; d = 11.7 ; cout << "Value of d : " << d << endl ; cout << "Value of d reference : " << s << endl ; return 0 ; }