二叉搜索树的操作集锦

总路线

⼆叉树算法的设计的总路线：明确⼀个节点要做的事情，然后剩下的事抛给框架。

void traverse(TreeNode root) { 
    // root 需要做什么？在这做。 
    // 其他的不⽤ root 操⼼，抛给框架 
    traverse(root.left); 
    traverse(root.right); 
}

如何把⼆叉树所有的节点中的值加⼀？

void plusOne(TreeNode root) { 
    if (root == null) return; 
    root.val += 1; 
    plusOne(root.left); 
    plusOne(root.right); 
}

如何判断两棵⼆叉树是否完全相同？

boolean isSameTree(TreeNode root1, TreeNode root2) { 
    // 都为空的话，显然相同 
    if (root1 == null && root2 == null) return true;
    // ⼀个为空，⼀个⾮空，显然不同 
    if (root1 == null || root2 == null) return false; 
    // 两个都⾮空，但 val 不⼀样也不⾏ 
    if (root1.val != root2.val) return false; 
    // root1 和 root2 该⽐的都⽐完了 
    return isSameTree(root1.left, root2.left) 
        && isSameTree(root1.right, root2.right); 
}

借助框架可以理解上述两个例子，那么就能解决所有二叉树算法。

二叉搜索树BST是一种很常用的二叉树，定义为：一个二叉树中，任意节点的值要大于等于左子树所有节点的值，且要小于等于右边子树所有节点的值。

基础操作有：判断合法性、增、删、查。

判断BST的合法性

这⾥是有坑的哦，我们按照刚才的思路，每个节点⾃⼰要做的事不就是⽐较⾃⼰和左右孩⼦吗？看起来应该这样写代码：

boolean isValidBST(TreeNode root) { 
    if (root == null) return true; 
    if (root.left != null && root.val <= root.left.val) return false; 
    if (root.right != null && root.val >= root.right.val) return false; 
    return isValidBST(root.left) 
        && isValidBST(root.right); 
}

但是这个算法出现了错误，BST 的每个节点应该要⼩于右边⼦树的所有节点，下⾯这个⼆叉树显然不是 BST，但是我们的算法会把它判定为 BST。出现错误，不要慌张，框架没有错，⼀定是某个细节问题没注意到。我们重新看⼀下 BST 的定义，root 需要做的不只是和左右⼦节点⽐较，⽽是要整个左⼦树和右⼦树所有节点⽐较。怎么办，鞭⻓莫及啊！

这种情况，我们可以使⽤辅助函数，增加函数参数列表，在参数中携带额外信息，请看正确的代码：

boolean isValidBST(TreeNode root) { 
    return isValidBST(root, null, null); 
}
boolean isValidBST(TreeNode root, TreeNode min, TreeNode max) { 
    if (root == null) return true; 
    if (min != null && root.val <= min.val) return false; 
    if (max != null && root.val >= max.val) return false; 
    return isValidBST(root.left, min, root) 
        && isValidBST(root.right, root, max); }

在BST中查找一个数是否存在

根据我们的指导思想，可以这样写代码：

boolean isInBST(TreeNode root, int target) { 
    if (root == null) return false; 
    if (root.val == target) return true; 
    
    return isInBST(root.left, target) || 
        isInBST(root.right, target); 
}

这样写完全正确，充分证明了你的框架性思维已经养成。现在你可以考虑⼀点细节问题了：如何充分利⽤信息，把 BST 这个“左⼩右⼤”的特性⽤上？很简单，其实不需要递归地搜索两边，类似⼆分查找思想，根据 target 和 root.val 的⼤⼩⽐较，就能排除⼀边。我们把上⾯的思路稍稍改动：

boolean isInBST(TreeNode root, int target) { 
    if (root == null) return false; 
    if (root.val == target) 
        return true; 
    if (root.val < target) 
        return isInBST(root.right, target);
    if (root.val > target) 
        return isInBST(root.left, target); 
    // root 该做的事做完了，顺带把框架也完成了，妙 
}

于是，我们对原始框架进⾏改造，抽象出⼀套针对 BST 的遍历框架：

void BST(TreeNode root, int target) { 
    if (root.val == target) 
        // 找到⽬标，做点什么 
    if (root.val < target) 
            BST(root.right, target);
    if (root.val > target) 
            BST(root.left, target); 
}

在 BST 中插⼊⼀个数

对数据结构的操作⽆⾮遍历 + 访问，遍历就是“找”，访问就是“改”。具体到这个问题，插⼊⼀个数，就是先找到插⼊位置，然后进⾏插⼊操作。

上⼀个问题，我们总结了 BST 中的遍历框架，就是“找”的问题。直接套框架，加上“改”的操作即可。⼀旦涉及“改”，函数就要返回 TreeNode 类型，并且对递归调⽤的返回值进⾏接收。

TreeNode insertIntoBST(TreeNode root, int val) { 
    // 找到空位置插⼊新节点 
    if (root == null) 
        return new TreeNode(val); 
    // if (root.val == val) 
    // BST 中⼀般不会插⼊已存在元素 
    if (root.val < val) 
        root.right = insertIntoBST(root.right, val); 
    if (root.val > val) 
        root.left = insertIntoBST(root.left, val); 
    return root; 
}

在 BST 中删除⼀个数

这个问题稍微复杂，不过你有框架指导，难不住你。跟插⼊操作类似，先“找”再“改”，先把框架写出来再说：

TreeNode deleteNode(TreeNode root, int key) { 
    if (root.val == key) { 
        // 找到啦，进⾏删除 
    } 
    else if (root.val > key) { 
        root.left = deleteNode(root.left, key); 
    } else if (root.val < key) { 
        root.right = deleteNode(root.right, key); 
    }
    return root; 
}

找到⽬标节点了，⽐⽅说是节点 A，如何删除这个节点，这是难点。因为删除节点的同时不能破坏 BST 的性质。有三种情况，⽤图⽚来说明。

情况 1：A 恰好是末端节点，两个⼦节点都为空，那么它可以当场去世了。

情况 2：A 只有⼀个⾮空⼦节点，那么它要让这个孩⼦接替⾃⼰的位置。

情况 3：A 有两个⼦节点，⿇烦了，为了不破坏 BST 的性质，A 必须找到左⼦树中最⼤的那个节点，或者右⼦树中最⼩的那个节点来接替⾃⼰。我们以第⼆种⽅式讲解。

三种情况分析完毕，填⼊框架，简化⼀下代码：

TreeNode deleteNode(TreeNode root, int key) { 
    if (root == null) return null; 
    if (root.val == key) { 
        // 这两个 if 把情况 1 和 2 都正确处理了 
        if (root.left == null) return root.right; 
        if (root.right == null) return root.left; 
        // 处理情况 3 
        TreeNode minNode = getMin(root.right); 
        root.val = minNode.val; 
        root.right = deleteNode(root.right, minNode.val); 
    } else if (root.val > key) { 
        root.left = deleteNode(root.left, key); 
    } else if (root.val < key) { 
        root.right = deleteNode(root.right, key); 
    }
    return root; 
}

TreeNode getMin(TreeNode node) { 
    // BST 最左边的就是最⼩的 
    while (node.left != null) node = node.left; 
    return node; 
}

删除操作就完成了。注意⼀下，这个删除操作并不完美，因为我们⼀般不会通过 root.val = minNode.val 修改节点内部的值来交换节点，⽽是通过⼀系列略微复杂的链表操作交换 root 和 minNode 两个节点。因为具体应⽤中，val 域可能会很⼤，修改起来很耗时，⽽链表操作⽆⾮改⼀改指针，⽽不会去碰内部数据。

但这⾥忽略这个细节，旨在突出 BST 基本操作的共性，以及借助框架逐层细化问题的思维⽅式。

总结

通过这篇⽂章，你学会了如下⼏个技巧：

1、⼆叉树算法设计的总路线：把当前节点要做的事做好，其他的交给递归

框架，不⽤当前节点操⼼。

2、如果当前节点会对下⾯的⼦节点有整体影响，可以通过辅助函数增⻓参

数列表，借助参数传递信息。

3、在⼆叉树框架之上，扩展出⼀套 BST 遍历框架：

void BST(TreeNode root, int target) { 
    if (root.val == target) ;
        // 找到⽬标，做点什么 
    if (root.val < target) 
            BST(root.right, target); 
    if (root.val > target) 
        BST(root.left, target); 
}

4、掌握了 BST 的基本操作。

快速计算完全⼆叉树的节点

如果让你数⼀下⼀棵普通⼆叉树有多少个节点，这很简单，只要在⼆叉树的遍历框架上加⼀点代码就⾏了。

但是，如果给你⼀棵完全⼆叉树，让你计算它的节点个数，你会不会？算法的时间复杂度是多少？这个算法的时间复杂度应该是 O(logN*logN)，如果你⼼中的算法没有达到⾼效，那么本⽂就是给你写的。

⾸先要明确⼀下两个关于⼆叉树的名词「完全⼆叉树」和「满⼆叉树」。我们说的完全⼆叉树如下图，每⼀层都是紧凑靠左排列的：我们说的满⼆叉树如下图，是⼀种特殊的完全⼆叉树，每层都是是满的，像⼀个稳定的三⾓形：

具体方法

如果是一个普通二叉树，显然只要向下面这样遍历一边即可，时间复杂度 O(N)：

public int countNodes(TreeNode root) {
    if (root == null) return 0;
    return 1 + countNodes(root.left) + countNodes(root.right);
}

那如果是一棵满二叉树，节点总数就和树的高度呈指数关系，时间复杂度 O(logN)：

public int countNodes(TreeNode root) {
    int h = 0;
    // 计算树的高度
    while (root != null) {
        root = root.left;
        h++;
    }
    // 节点总数就是 2^h - 1
    return (int)Math.pow(2, h) - 1;
}

完全二叉树比普通二叉树特殊，但又没有满二叉树那么特殊，计算它的节点总数，可以说是普通二叉树和完全二叉树的结合版，先看代码：

public int countNodes(TreeNode root) {
    TreeNode l = root, r = root;
    // 记录左、右子树的高度
    int hl = 0, hr = 0;
    while (l != null) {
        l = l.left;
        hl++;
    }
    while (r != null) {
        r = r.right;
        hr++;
    }
    // 如果左右子树的高度相同，则是一棵满二叉树
    if (hl == hr) {
        return (int)Math.pow(2, hl) - 1;
    }
    // 如果左右高度不同，则按照普通二叉树的逻辑计算
    return 1 + countNodes(root.left) + countNodes(root.right);
}

结合刚才针对满二叉树和普通二叉树的算法，上面这段代码应该不难理解，就是一个结合版，但是其中降低时间复杂度的技巧是非常微妙的。

复杂度分析

开头说了，这个算法的时间复杂度是 O(logNlogN)，这是怎么算出来的呢？直觉感觉好像最坏情况下是 O(NlogN) 吧，因为之前的 while 需要 logN 的时间，最后要 O(N) 的时间向左右子树递归：

1	return 1 + countNodes(root.left) + countNodes(root.right);

关键点在于，这两个递归只有一个会真的递归下去，另一个一定会触发hl == hr而立即返回，不会递归下去。

为什么呢？原因如下：

一棵完全二叉树的两棵子树，至少有一棵是满二叉树：

看图就明显了吧，由于完全二叉树的性质，其子树一定有一棵是满的，所以一定会触发hl == hr，只消耗 O(logN) 的复杂度而不会继续递归。

综上，算法的递归深度就是树的高度 O(logN)，每次递归所花费的时间就是 while 循环，需要 O(logN)，所以总体的时间复杂度是 O(logN*logN)。所以说，「完全二叉树」这个概念还是有它存在的原因的，不仅适用于数组实现二叉堆，而且连计算节点总数这种看起来简单的操作都有高效的算法实现。

如何使用单调栈解题

单调栈实际上就是栈，只是利⽤了⼀些巧妙的逻辑，使得每次新元素⼊栈后，栈内的元素都保持有序（单调递增或单调递减）。听起来有点像堆（heap）？不是的，单调栈⽤途不太⼴泛，只处理⼀种典型的问题，叫做 Next Greater Element。本⽂⽤讲解单调队列的算法模版解决这类问题，并且探讨处理「循环数组」的策略。

题目

⾸先，讲解 Next Greater Number 的原始问题：给你⼀个数组，返回⼀个等⻓的数组，对应索引存储着下⼀个更⼤元素，如果没有更⼤的元素，就存 -1。不好⽤语⾔解释清楚，直接上⼀个例⼦：

给你⼀个数组 [2,1,2,4,3]，你返回数组 [4,2,4,-1,-1]。

解释：第⼀个 2 后⾯⽐ 2 ⼤的数是 4; 1 后⾯⽐ 1 ⼤的数是 2；第⼆个 2 后⾯⽐ 2 ⼤的数是 4; 4 后⾯没有⽐ 4 ⼤的数，填 -1；3 后⾯没有⽐ 3 ⼤的数，填 -1。这道题的暴⼒解法很好想到，就是对每个元素后⾯都进⾏扫描，找到第⼀个更⼤的元素就⾏了。但是暴⼒解法的时间复杂度是 O(n^2)。

解法

这个问题可以这样抽象思考：把数组的元素想象成并列站⽴的⼈，元素⼤⼩想象成⼈的⾝⾼。这些⼈⾯对你站成⼀列，如何求元素「2」的 Next Greater Number 呢？很简单，如果能够看到元素「2」，那么他后⾯可⻅的第⼀个⼈就是「2」的 Next Greater Number，因为⽐「2」⼩的元素⾝⾼不够，都被「2」挡住了，第⼀个露出来的就是答案。

这个情景很好理解吧？带着这个抽象的情景，先来看下代码

vector<int> nextGreaterElement(vector<int>& nums) { 
    vector<int> ans(nums.size()); 
    // 存放答案的数组 
    stack<int> s; 
    for (int i = nums.size() - 1; i >= 0; i--) { 
        // 倒着往栈⾥放 
        while (!s.empty() && s.top() <= nums[i]) { 
            // 判定个⼦⾼矮 
            s.pop(); // 矮个起开，反正也被挡着了。。。 
        }
        ans[i] = s.empty() ? -1 : s.top(); // 这个元素⾝后的第⼀个⾼个 
        s.push(nums[i]); 
        // 进队，接受之后的⾝⾼判定吧！ 
    }
    return ans; 
}

这就是单调队列解决问题的模板。for 循环要从后往前扫描元素，因为我们借助的是栈的结构，倒着⼊栈，其实是正着出栈。while 循环是把两个“⾼个”元素之间的元素排除，因为他们的存在没有意义，前⾯挡着个“更⾼”的元素，所以他们不可能被作为后续进来的元素的 Next Great Number 了。这个算法的时间复杂度不是那么直观，如果你看到 for 循环嵌套 while 循环，可能认为这个算法的复杂度也是 O(n^2)，但是实际上这个算法的复杂度只有 O(n)

时间复杂度

分析它的时间复杂度，要从整体来看：总共有 n 个元素，每个元素都被 push ⼊栈了⼀次，⽽最多会被 pop ⼀次，没有任何冗余操作。所以总的计算规模是和元素规模 n 成正⽐的，也就是 O(n) 的复杂度。

给你⼀个数组 T = [73, 74, 75, 71, 69, 72, 76, 73]，这个数组存放的是近⼏天的天⽓⽓温（这⽓温是铁板烧？不是的，这⾥⽤的华⽒度）。你返回⼀个数组，计算：对于每⼀天，你还要⾄少等多少天才能等到⼀个更暖和的⽓温；如果等不到那⼀天，填 0 。

举例：给你 T = [73, 74, 75, 71, 69, 72, 76, 73]，你返回 [1, 1, 4, 2, 1, 1, 0, 0]。

解释：第⼀天 73 华⽒度，第⼆天 74 华⽒度，⽐ 73 ⼤，所以对于第⼀天，只要等⼀天就能等到⼀个更暖和的⽓温。后⾯的同理。你已经对 Next Greater Number 类型问题有些敏感了，这个问题本质上也是找 Next Greater Number，只不过现在不是问你 Next Greater Number 是多少，⽽是问你当前距离 Next Greater Number 的距离⽽已。相同类型的问题，相同的思路，直接调⽤单调栈的算法模板，稍作改动就可以啦，直接上代码把

vector<int> dailyTemperatures(vector<int>& T) { 
    vector<int> ans(T.size()); 
    stack<int> s; // 这⾥放元素索引，⽽不是元素 
    for (int i = T.size() - 1; i >= 0; i--) { 
        while (!s.empty() && T[s.top()] <= T[i]) { 
            s.pop(); 
        }
        ans[i] = s.empty() ? 0 : (s.top() - i); 
        // 得到索引间距 
        s.push(i); 
        // 加⼊索引，⽽不是元素 
    }
    return ans; 
}

扩展问题：循环数组

单调栈讲解完毕。下⾯开始另⼀个重点：如何处理「循环数组」。

同样是 Next Greater Number，现在假设给你的数组是个环形的，如何处理？

给你⼀个数组 [2,1,2,4,3]，你返回数组 [4,2,4,-1,4]。拥有了环形属性，最后⼀个元素 3 绕了⼀圈后找到了⽐⾃⼰⼤的元素 4 。

⾸先，计算机的内存都是线性的，没有真正意义上的环形数组，但是我们可以模拟出环形数组的效果，⼀般是通过 % 运算符求模（余数），获得环形特效

int[] arr = {1,2,3,4,5}; 
int n = arr.length, index = 0; 
while (true) { 
    print(arr[index % n]); 
    index++; 
}

回到 Next Greater Number 的问题，增加了环形属性后，问题的难点在于：

这个 Next 的意义不仅仅是当前元素的右边了，有可能出现在当前元素的左边（如上例）。

明确问题，问题就已经解决了⼀半了。我们可以考虑这样的思路：将原始数组“翻倍”，就是在后⾯再接⼀个原始数组，这样的话，按照之前“⽐⾝⾼”的流程，每个元素不仅可以⽐较⾃⼰右边的元素，⽽且也可以和左边的元素⽐较了

怎么实现呢？你当然可以把这个双倍⻓度的数组构造出来，然后套⽤算法模板。但是，我们可以不⽤构造新数组，⽽是利⽤循环数组的技巧来模拟。直接看代码吧：

vector<int> nextGreaterElements(vector<int>& nums) { 
    int n = nums.size(); 
    vector<int> res(n); 
    // 存放结果 
    stack<int> s; 
    // 假装这个数组⻓度翻倍了 
    for (int i = 2 * n - 1; i >= 0; i--) { 
        while (!s.empty() && s.top() <= nums[i % n]) 
            s.pop(); 
        res[i % n] = s.empty() ? -1 : s.top(); 
        s.push(nums[i % n]); 
    }
    return res; 
}

利用单调队列解题

前⽂讲了⼀种特殊的数据结构「单调栈」monotonic stack，解决了⼀类问题「Next Greater Number」，本⽂写⼀个类似的数据结构「单调队列」。也许这种数据结构的名字你没听过，其实没啥难的，就是⼀个「队列」，只是使⽤了⼀点巧妙的⽅法，使得队列中的元素单调递增（或递减）。这个数据结构有什么⽤？可以解决滑动窗⼝的⼀系列问题

题目

给定一个数组nums，有一个大小为k的滑动窗口从数组的最左侧移动到数组的最右侧；你只可以看到在滑动窗口k内的数字，滑动窗口每次只向右移动一位，返回滑动窗口最大值。

二叉堆详解

⼆叉堆（Binary Heap）没什么神秘，性质⽐⼆叉搜索树 BST 还简单。其主要操作就两个， sink （下沉）和 swim （上浮），⽤以维护⼆叉堆的性质。其主要应⽤有两个，⾸先是⼀种排序⽅法「堆排序」，第⼆是⼀种很有⽤的数据结构「优先级队列」。

本⽂就以实现优先级队列（Priority Queue）为例，通过图⽚和⼈类的语⾔来描述⼀下⼆叉堆怎么运作的

概述

⼆叉堆其实就是⼀种特殊的⼆叉树（完全⼆叉树），只不过存储在数组⾥。⼀般的链表⼆叉树，我们操作节点的指针，⽽在数组⾥，我们把数组索引作为指针：

// ⽗节点的索引 
int parent(int root) { 
    return root / 2; 
}
// 左孩⼦的索引 
int left(int root) { 
    return root * 2; 
}
// 右孩⼦的索引 
int right(int root) { 
    return root * 2 + 1; 
}

画个图你⽴即就能理解了，注意数组的第⼀个索引 0 空着不⽤，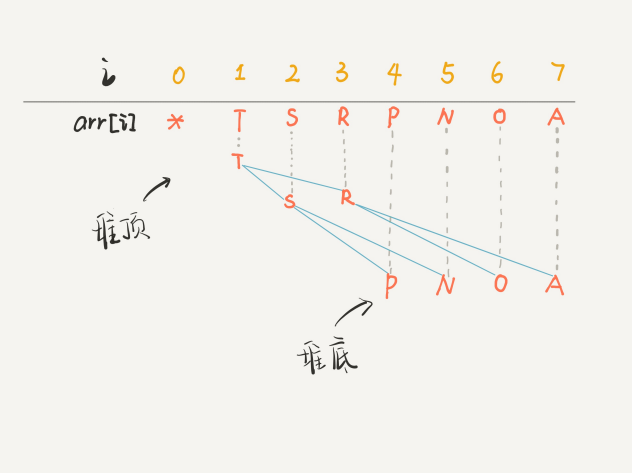

PS：因为数组索引是数组，为了⽅便区分，将字符作为数组元素。

你看到了，把 arr[1] 作为整棵树的根的话，每个节点的⽗节点和左右孩⼦的索引都可以通过简单的运算得到，这就是⼆叉堆设计的⼀个巧妙之处。为了⽅便讲解，下⾯都会画的图都是⼆叉树结构，相信你能把树和数组对应起来

⼆叉堆还分为最⼤堆和最⼩堆。最⼤堆的性质是：每个节点都⼤于等于它的 两个⼦节点。类似的，最⼩堆的性质是：每个节点都⼩于等于它的⼦节点。两种堆核⼼思路都是⼀样的，本⽂以最⼤堆为例讲解。对于⼀个最⼤堆，根据其性质，显然堆顶，也就是 arr[1] ⼀定是所有元素中最⼤的元素。

优先级队列

优先级队列这种数据结构有⼀个很有⽤的功能，你插⼊或者删除元素的时候，元素会⾃动排序，这底层的原理就是⼆叉堆的操作。

数据结构的功能⽆⾮增删查该，优先级队列有两个主要 API，分别是 insert 插⼊⼀个元素和 delMax 删除最⼤元素（如果底层⽤最⼩堆，那么就是 delMin ）。

下⾯我们实现⼀个简化的优先级队列，先看下代码框架： PS：为了清晰起⻅，这⾥⽤到 Java 的泛型， Key 可以是任何⼀种可⽐较⼤⼩的数据类型，你可以认为它是 int、char 等。

public class MaxPQ 
    <Key extends Comparable<Key>> { 
    // 存储元素的数组 
    private Key[] pq; 
    // 当前 Priority Queue 中的元素个数 
    private int N = 0; public MaxPQ(int cap) { 
        // 索引 0 不⽤，所以多分配⼀个空间 
        pq = (Key[]) new Comparable[cap + 1]; 
    }
    
    /* 返回当前队列中最⼤元素 */ 
    public Key max() { 
        return pq[1]; 
    }
    /* 插⼊元素 e */ 
    public void insert(Key e) {...} 
    
    /* 删除并返回当前队列中最⼤元素 */ 
    public Key delMax() {...} 
   
    /* 上浮第 k 个元素，以维护最⼤堆性质 */ 
    private void swim(int k) {...} 
    
    /* 下沉第 k 个元素，以维护最⼤堆性质 */ 
    private void sink(int k) {...}
    
    /* 交换数组的两个元素 */ 
    private void exch(int i, int j) { 
        Key temp = pq[i]; 
        pq[i] = pq[j]; 
        pq[j] = temp; 
    }
    
    /* pq[i] 是否⽐ pq[j] ⼩？ */ 
    private boolean less(int i, int j) { 
        return pq[i].compareTo(pq[j]) < 0; 
    }
    /* 还有 left, right, parent 三个⽅法 */ 
}

空出来的四个⽅法是⼆叉堆和优先级队列的奥妙所在，下⾯⽤图⽂来逐个理解

swim和sink

为什么要有上浮 swim 和下沉 sink 的操作呢？为了维护堆结构。我们要讲的是最⼤堆，每个节点都⽐它的两个⼦节点⼤，但是在插⼊元素和删除元素时，难免破坏堆的性质，这就需要通过这两个操作来恢复堆的性质了。

对于最⼤堆，会破坏堆性质的有有两种情况：

1、如果某个节点 A ⽐它的⼦节点（中的⼀个）⼩，那么 A 就不配做⽗节点，应该下去，下⾯那个更⼤的节点上来做⽗节点，这就是对 A 进⾏下沉。

2、如果某个节点 A ⽐它的⽗节点⼤，那么 A 不应该做⼦节点，应该把⽗节点换下来，⾃⼰去做⽗节点，这就是对 A 的上浮。

当然，错位的节点 A 可能要上浮（或下沉）很多次，才能到达正确的位置，恢复堆的性质。所以代码中肯定有⼀个 while 循环。

细⼼的读者也许会问，这两个操作不是互逆吗，所以上浮的操作⼀定能⽤下沉来完成，为什么我还要费劲写两个⽅法？是的，操作是互逆等价的，但是最终我们的操作只会在堆底和堆顶进⾏（等会讲原因），显然堆底的「错位」元素需要上浮，堆顶的「错位」元素需要下沉

上浮的代码实现：

private void swim(int k) { 
    // 如果浮到堆顶，就不能再上浮了 
    while (k > 1 && less(parent(k), k)) { 
        // 如果第 k 个元素⽐上层⼤ 
        // 将 k 换上去 
        exch(parent(k), k); 
        k = parent(k); 
    } 
}

下沉的代码实现：

private void sink(int k) { 
    // 如果沉到堆底，就沉不下去了 
    while (left(k) <= N) { 
        // 先假设左边节点较⼤ 
        int older = left(k); 
        // 如果右边节点存在，⽐⼀下⼤⼩ 
        if (right(k) <= N && less(older, right(k))) 
            older = right(k); 
        // 结点 k ⽐俩孩⼦都⼤，就不必下沉了 
        if (less(older, k)) break;
        // 否则，不符合最⼤堆的结构，下沉 k 结点 
        exch(k, older); 
        k = older; 
    } 
}

⾄此，⼆叉堆的主要操作就讲完了，⼀点都不难吧，代码加起来也就⼗⾏。明⽩了 sink 和 swim 的⾏为，下⾯就可以实现优先级队列了

实现 delMax 和 insert

这两个⽅法就是建⽴在 swim 和 sink 上的。 insert ⽅法先把要插⼊的元素添加到堆底的最后，然后让其上浮到正确位 置。

public void insert(Key e) { 
    N++; 
    // 先把新元素加到最后 
    pq[N] = e; 
    // 然后让它上浮到正确的位置 
    swim(N); 
}

delMax ⽅法先把堆顶元素 A 和堆底最后的元素 B 对调，然后删除 A**，最** 后让 B 下沉到正确位置。

public Key delMax() { 
    // 最⼤堆的堆顶就是最⼤元素 
    Key max = pq[1]; 
    // 把这个最⼤元素换到最后，删除之 
    exch(1, N);
    pq[N] = null; 
    N--; 
    // 让 pq[1] 下沉到正确位置 
    sink(1); 
    return max; 
}

⾄此，⼀个优先级队列就实现了，插⼊和删除元素的时间复杂度为 O(logK) ， K 为当前⼆叉堆（优先级队列）中的元素总数。因为我们时间复杂度主要花费在 sink 或者 swim 上，⽽不管上浮还是下沉，最多也就树（堆）的⾼度，也就是 log 级别

总结

⼆叉堆就是⼀种完全⼆叉树，所以适合存储在数组中，⽽且⼆叉堆拥有⼀些特殊性质。

⼆叉堆的操作很简单，主要就是上浮和下沉，来维护堆的性质（堆有序），核⼼代码也就⼗⾏。

优先级队列是基于⼆叉堆实现的，主要操作是插⼊和删除。插⼊是先插到最后，然后上浮到正确位置；删除是调换位置后再删除，然后下沉到正确位置。核⼼代码也就⼗⾏。

也许这就是数据结构的威⼒，简单的操作就能实现巧妙的功能，真⼼佩服发明⼆叉堆算法的⼈！

Technical blog

数据结构算法