Technical blog

IT小白的成长之旅

0%

发表于 更新于 分类于

动态规划框架

动态规划问题的一般形式是求最值；求解动态规划的核心问题是穷举，肯定要把所有可行的答案穷举出来然后在其中找最值；且一般具有重叠子问题，需要备忘录或者DP table来优化。

关键：状态转移方程，明确[状态]->定义DP数组、函数的含义->明确[选择]->明确basecase。

带备忘录的递归，有时候耗时的原因是重复计算，那么可以造备忘录，每次算出某子问题后不急着返回，先记到备忘录中；每次遇到一个子问题时，先去备忘录查一查，如果发现已经解决过，就直接拿出来用。

一般使用一个数组充当备忘录，当然也可以使用hash表，思想是一样的。

斐波那契数列问题：

1
2
3
4
5
6
7
8
const fit = (N) => {
    if (N < 1) return 0;
    var memo = new Array(N + 1);
    memo[1] = memo[2] = 1;
    for (let i = 3; i <= N; i++)
        memo[i] = memo[i-1] + memo[i - 2];
    return memo[N];
}

带备忘录的递归解法和迭代的动态规划解法其实一样，递归自顶向下，迭代递归自底向上；

动态规划的另一个重要特性：最优子结构；凑零钱问题：给你k种面值的硬币，面值分别为C1、C2、…Ck；再给一个总金额amount，问最少需要多少硬币凑出，如果不能凑出则返回-1。

要符合最优子结构，子问题之间必须相互独立，状态转移方程的步骤

1、确定状态，也就是原问题和子问题变化的变量，唯一状态为目标金额amount；

2、确定dp函数的定义：当前目标金额为n，则至少需要dp(n)个硬币；

3、确定选择并择优：对于每个状态，可以做出选择改变当前状态；具体至当前，无论目标金额多少，选择就是从面额列表coins种选择一个硬币，然后目标金额就会减少。

4、最后明确base case，显然目标金额为0时，所需硬币数量为0；当目标金额小于0时，无解，返回-1。

一般这种题需要使用备忘录来消除子问题，减少其冗余从而节省时间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
const coinChange = (coins, amount){
    let memo = [];
    const dp = (n) => {
        if (memo[n] != null) return memo[n];
        //先查备忘录，避免重复计算
        if (n == 0) return 0;
        if (n < 0) return -1;
        res = MAX_VALUE;
        for (let i = 0; i < coins.length; i++){
            let subproblem == dp(n - coins[i]);
            if (subproblem == -1) continue;
            res = min(res, 1 + subproblem);
        }
        if (res != MAX_VALUE){
            memo[n] = res;
        }
        else memo[n] = -1;
        return memo[n];
    }
    return dp(amount);
}

除了这种自顶向下的带备忘录递归，自底向上的dp数组迭代也一样可以消除子问题：dp[i] = x，表示当目标金额为i时，至少需要x枚硬币。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
const coinChange = (coins, amount) =>{
    let dp = new Array(amount + 1);
    for (let i = 0; i < amount + 1; i++){
        dp[i] = amount + 1;
    }
    //先初始化dp数组，长度与初始值
    for (i = 0; i < dp.length; i++){
        //内层for在求所有子问题+1的最小值
        for (let j = 0; j < coins.length; j++){
            //子问题无解则跳过
            if (i - coins[j] < 0) continue;
            dp[i] = min(dp[i], 1 + dp[i - coin]);
        }
    }
    if (dp[amount] == amount + 1) return -1;
    else return dp[amount];
}

动态规划之背包问题

给你一个则装载重量为W的背包和N个物品，每个物品有重量和价值两个属性，其中第i个物品重量为wt[i]，价值为val[i]，求使用该背包装物品的最大价值。

典型动态规划：物品不可分割，要么装进包里，要么不装，不可能切分。解决这种问题没有排序的巧妙方法，只能穷举所有可能，根据动态规划套路走流程：

1、明确状态与选择；状态：背包容量与可选择的物品；选择：装进背包或不装进背包。

1
2
3
4
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ....
            dp[状态1][状态2][...] = 择优(选择1， 选择2， ...)

2、明确DP数组：描述当前问题局面，需要使用DP数组把状态表示出来，而状态有2个，因此为二维数组dp[i] [w] :对于前i个物品，当前背包的容量为w，这种情况下可以装的最大价值为dp[i] [w]。且base case 就是dp[0] [..] = dp[..] [0] = 0。

3、根据选择，思考状态转移的逻辑：即把物品i装不装进背包的代码逻辑怎么体现。如果不装：dp[i] [w] = dp[i-1] [w]，即继承以前的结果；如果装：dp[i] [w] = dp[i-1] [w - wt[i-1]] + val[i-1]，在装第i个的前提下该如何最大价值，应寻求剩余重量w - wt[i-1]限制下的最大重量，再加上确定的第i个物品价值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
const knapsack = (W, N, wt, val) =>{
    let dp = new Array();
    for (let i = 0; i < N + 1; i++){
        dp[i] = new Array();
        for (let j = 0; j < W + 1; j++){
            dp[i][j] = 0;
        }
    }//先定义二维数组，并均初始化为0
    for (i = 1; i <= N; i++){
        for (w = 1; w <= W; W++){
            if (w - wt[i - 1] < 0){
                //当前背包容量放不下时，只能选择不装入背包
                dp[i][w] = dp[i - 1][w];
            } else {
                //装入或不装入背包的择优
                dp[i][w] = max(dp[i - 1][w - wt[i - 1]] + val[i - 1], dp[i - 1][w]);
            }
        }
    }
    return dp[N][W];
}
//使用动态规划遍历时，同时择优并用DP表来存储已经计算完的数据。

动态规划之子集背包分割

怎么将⼆维动态规划压缩成⼀维动态规划吗？这就是状态压缩，很容易的，

题目：给定一个只包含正整数的非空数组，是否可以将该数组分割成两个子集，使两个子集的元素和相等：

对于这个问题，看起来和背包没有任何关系，为什么说它是背包问题呢？ ⾸先回忆⼀下背包问题⼤致的描述是什么： 给你⼀个可装载重量为 W 的背包和 N 个物品，每个物品有重量和价值两 个属性。其中第 i 个物品的重量为 wt[i] ，价值为 val[i] ，现在让你⽤ 这个背包装物品，最多能装的价值是多少？

那么对于这个问题，我们可以先对集合求和，得出 sum ，把问题转化为背 包问题：给⼀个可装载重量为 sum / 2 的背包和 N 个物品，每个物品的重量为 nums[i] 。现在让你装物品，是否存在⼀种装法，能够恰好将背包装满？

你看，这就是背包问题的模型，甚⾄⽐我们之前的经典背包问题还要简单⼀ 些，下⾯我们就直接转换成背包问题，开始套前⽂讲过的背包问题框架即就可。

1、明确状态与选择；状态：背包容量、可选择的物品；选择：是否装进背包

2、dp数组定义：dp[ i ] [ j ]= x 表⽰，对于前 i 个物品，当前背包的容量为 j 时，若 x 为 true ，则说明可以恰好将背包装满，若 x 为 false ，则说明不能恰 好将背包装满。

3、根据选择来思考状态转移的逻辑，恰好把背包装满的条件，其实刚好又取决于其上一个状态；换句话说，如果 j - nums[i-1] 的重量可以被恰好装满，那么只要把第 i 个物品装进去，也可恰好装满 j 的重量；否则的话，重量 j 肯定是装不满的。

4、basecase：想求的最终答案是dp[N] [sum/2]，因此初始条件为dp[…] [0] = true和dp[0] […] = false；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
const canPartition = (nums) => {
    let sum = 0;
    for (let i = 0; i < nums.length; i++){
        sum += nums[i];
    }
    if (sum % 2 != 0) return false;
    let len = nums.length;
    sum = sum / 2;
    let dp = new Array();
    
    //根据初始条件来初始化
    for (i = 0; i <= len + 1; i++) {
        dp[i] = new Array();
        for (let j = 0; j <= sum + 1; j++){
            dp[i][j] = false;
        }
    }
    for (i = 0; i <= n; i++){
        dp[i] [0] = true;
    }
    
    for (i = 0; i <= n; i++){
        for (j = 0; j <= sum; j++){
            if (j - nums[i - 1] < 0){
                //背包不足，不能装入第i个物品
                dp[i] [j] = dp[i - 1] [j];
            } else {
                //装入或不装入的选择
                dp[i][j] = dp[i - 1] [j] | dp[i - 1] [j - nums[i - 1]];
            }
        }
    }
    return dp[n] [sum];
}

动态规划之零钱兑换（完全背包问题）

题目：给定不同面额的硬币和一个总金额，假设每种硬币有无数个，写出函数来计算能凑成总金额的硬币总和数。

有⼀个背包，最⼤容量为 amount ，有⼀系列物品 coins ，每个物品的重量为 coins[i] ，每个物品的数量⽆限。请问有多少种⽅法，能够把背包恰 好装满？

这个问题和我们前⾯讲过的两个背包问题，有⼀个最⼤的区别就是，每个物 品的数量是⽆限的，这也就是传说中的「完全背包问题」，没啥⾼⼤上的， ⽆⾮就是状态转移⽅程有⼀点变化⽽已。

1、状态与选择；状态：背包的容量，可选择的物品；选择：是否装进背包；

2、dp数组：若只使用前i个物品，当背包容量为j时，有dp[i] [j]种方法可以装满背包；

3、base case为dp[0] [..] = 0;dp[..] [0] = 1;不使用任何面值则无法完成，背包容量为0则仅有一种。

4、状态转移方程的逻辑：如果不把第i个物品装进背包，则凑出面额j的方法数dp[i] [j]等于dp[i - 1] [j]，继承之前的结果；如果你把第i个物品装进了背包，则说明使用了coins[i - 1] 这个面额，那么dp[i] [j] = dp [i] [j-coins[i - 1]]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
const change = (amount, coins) => {
    let len = coins.length;
    let dp = new Array();
    
    //根据初始条件来初始化
    for (let i = 0; i <= len + 1; i++) {
        dp[i] = new Array();
        for (let j = 0; j <= sum + 1; j++){
            dp[i][j] = 0;
        }
    }
    for (i = 0; i <= n; i++){
        dp[i] [0] = 1;
    }
    for (i = 1; i <=n; i++){
        for (j = 1; j <= amount; j++){
            if (j - coins[i - 1] >= 0) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i - 1]];
            } else {
                dp[i][j] = dp[i - 1][j];
            }
        }
    }
    return dp[n][amount];
}

动态规划最长递增子序列

动态规划的通用技巧：数学归纳思想；最长递增子序列LIS；子串与子序列名词的区别：字串一定是连续的，而子序列不一定是连续的。

1、明确状态与选择：状态，序列nums的所有字母；选择：更新子序列还是

2、用dp数组来描述状态，dp[i]表示以nums[i]这个数结尾的最长递增子序列的长度；后续的动态规划子序列解题模板总结了常见的套路:

3、根据选择思考动态转移方程的逻辑：已知dp[0..n-1]，根据nums[n]的值，便能够判断如何更新，找到结尾比nums[n]小的子序列，然后把nums[n]接到最后，形成新子序列，其长度为原子序列+1；且由于未知之前子序列的大小关系，需要使用遍历将前面的dp值全部遍历一遍；

4、base case: dp[i]初始值为1，因为以nums[i]结尾的LIS最少要包含它自己。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
const lengthOfLIS = (nums) => {
    let dp = new Array();
    for (let i = 0; i < nums.length; i++){
        dp[i] = 1;
    }
    for (i = 0; i < nums.length; i++){
        for (let j = 0; j < i; j++){
            if (nums[i] > nums[j]){
                dp[i] = max.(dp[i], dp[j] + 1);
            }
        }
    }
    let res = 0;
    //将每个以nums[i]结尾的LIS长度存到dp之后，遍历一遍找出最大的那个
    for (i = 0; i < dp.length; i++){
        res = max.(res, dp[i]);
    }
    return res;
}

动态规划：最长公共子序列LCS

LCS是典型的二维动态规划，目的是求两个字符串的LCS长度，子序列问题基本都用动态规划来实现，穷举加剪枝。

1、明确状态与选择：状态，两个字符串；选择，是否添加该元素作为最长公共子序列。

2、确定dp数组的含义： 两字符串数组的通用套路，dp[i] [j]代表s1[1…i]和s2[1…j]的LCS长度。

3、找状态转移方程：其实字符串问题的状态转移套路都差不多，都是判断字符在还是不在的问题，只有2种选择；如果某字符在LCS中，则其肯定同时存在于s1和s2中。

思路为：用2个指针从后往前遍历s1、s2，若相等则该字符一定在lcs中，否则这两个字符至少有一个不在lcs中，需要丢弃一个；

4、base case：均初始化为0，最短可以没有公共元素。

暴力的递归写法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
const longestCommonSubsequence = (str1, str2) => {
    const dp = (let i , let j) => {
        if (i === -1 || j === -1) return 0;
        //先初始化空串的base case
        if (str1[i] === str[j]){
            //找到一个lcs的元素则继续往前找
            return dp(i - 1, j - 1) + 1;
        } else{
            //否则，则找出让lcs最长的
            return max(dp(i - 1, j), dp(i, j - 1));
        }
    }
    return dp(str1.length - 1, str2.length - 1);
}

可以通过备忘录或者DPtable来优化时间复杂度，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
const longestCommonSubsequencr = (str1, str2) => {
    let m = str1.length, n = str2.length;
    let dp = new Array();
    for (let i = 0; i < m; i++){
        dp[i] = new Array();
        for (let j = 0; j < n; j++){
            dp[i][j] = 0; 
        }
    }
    //构建DPtable并初始化
    for (i = 0; i < m; i++){
        for (j = 0; j < n; j++){
            if (str[i] === str[j]){
                dp[i][j] = 1 + dp[i - 1][j - 1];
            } else{
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    return dp[m - 1][n - 1];
}

对于str1[i]与str2[j]不等的情况，是否可能两个字符都不在，但其实因为后面的选择max始终选择最大的，因此不用考虑，必然被排除在外。先像文本一样写出伪代码来定义DPtable理清逻辑，思考每个状态有哪些选择，用正确逻辑作出正确判断就能做出正确选择。

经典动态规划：编辑距离

给定两个字符串s1和s2，计算出将s1转换成s2所使用的最少操作数，可用操作只有插入、删除、替换一个字符。

思路：解决两个字符串的动态规划问题，一般都是用2个指针i、j分别指向两个字符串的最后，然后一步步往前走，缩小问题的规模；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/*base case:当i走完s1或者j走完s2时，可以直接返回另一个字符串剩下的长度；
if s1[i] == s2[j]:
    啥也不做(skip)
    i、j同时移动
else:
    三选一：
        插入、删除、替换
三选一选择的标准是：均尝试一遍，哪个操作最后得到的编辑距离最小。*/
const minDistance = (s1, s2) => {
    const dp = (i, j) =>{
        if (i == -1) return j + 1;
        if (j == -1) return i + 1;
        //定义base case
        if (s1[i] == s2[j]) return dp(i - 1, j - 1);
        else return min(dp(i, j - 1) + 1，dp(i - 1, j) + 1, dp(i - 1, j - 1) + 1);
    }
    return dp(s1.length - 1, s2.length - 1);
}

dp(i, j)返回s1[0..i]和s2[0..j]的最小编辑距离；同样，上述的解法属于暴力破解，需要使用动态规划技巧来优化重叠子问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
const minDistance = (s1, s2) => {
    let m = str1.length, n = str2.length;
    let dp = new Array();
    for (let i = 0; i < m; i++){
        dp[i] = new Array();
        for (let j = 0; j < n; j++){
            dp[i][j] = 0; 
        }
    }
    //构建DPtable并初始化
    for (int i = 1; i <= m; i++){
        dp[i][0] = i;
    }
    for (int j = 1; j <= n; j++){
        dp[0][j] = j;
    }
    //进行合适的DPtable初始化，DPtable自底向上求解，递归从上至下
    for (i = 1; i <= m; i++){
        for (j = 1; j <= n; j++){
            if (s1[i] === s2[j]){
                dp[i][j] = dp[i - 1][j - 1];
            } else{
                dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + 1);
            }
        }
    }
    return dp[m][n];
}

一般来说，处理两个字符串的动态规划问题，均按照本文思路处理，建立DPtable；但这里仅给出了最小编辑距离，具体如何修改则需要给dp数组增加额外的信息。则使用JS中的对象数组，dp[i] [j]中存储的是一个对象

1
2
3
4
5
6
7
8
9
10
11
12
13
14
let arrayObj = [{}];//定义对象数组
let m = str1.length, n = str2.length;
    let dp = new Array();
    for (let i = 0; i < m; i++){
        dp[i] = new Array();
        for (let j = 0; j < n; j++){
            dp[i][j] = {
                'val' : 0,
                'choice' : 0,
                //val为其原本dp数组值，choice为操作，0代表什么也不做，1代表插入，2代表删除，3代表替换
            }; 
        }
    }
//最终结果为dp[m][n]，后续则一步步反推，插入=>左移、替换=>左移并上移、删除=>上移,形成一条路径；这样一步步走回来了。

动态规划的子序列模板（最长回文子序列）

子序列通常涉及两个字符串，例如：两个字符串的最长公共子序列；既然要用动态规划，关键在于dp数组的定义与寻找状态转移关系，不同问题需要使用不同的dp数组定义。

一、一维的dp数组

最长递增子序列LIS：在子数组array[0…i]中，以array[i]为结尾的目标子序列的长度是dp[i]。

目的：符合归纳法，能够从前n-1个的结果中推断出来第n个的结果

二、二维的dp数组

涉及两个字符串、数组时：

在子数组arr1[0…i]和子数组arr2[0…j]中，我们要求的子序列(最长公共子序列)长度为dp[i] [j];

只涉及一个字符串、数组：

在子数组array[i…j]中，我们要求的子序列(最长回文子序列)的长度为dp[i] [j]。

最长回文子序列

DPtable的定义：在子串s[i…j]中，最长回文子序列的长度为dp[i] [j]；找状态转移方程的关键在于归纳思维，即如何从已知的结果推断出未知的部分。

具体来说，如果我们想求dp[i] [j]，假设已经知道子问题dp[i + 1] [j - 1]的结果，是否能想办法算出dp[i] [j]的值。可以，取决于s[i]和s[j]的字符。1、如果他两相等则它们加上便就是当前的最大回文子序列；2、如果她两不相等，说明两者不可能同时出现在最长回文子序列中，于是把它们分别加入s[i+1…j-1]中，看看哪个子串产生的回文子序列更长即可。

base case：dp[i] [j] = 1;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
const longestPalindromeSubseq = (str1) => {
    let m = str1.length;
    let dp = new Array();
    for (let i = 0; i < m; i++){
        dp[i] = new Array();
        for (let j = 0; j < n; j++){
            dp[i][j] = 0; 
        }
    }
    for (i = 0; i < n; i++){
        dp[i][i] = 1;
    }
    //根据上面的状态转移方程，为保证每次计算dp[i][j]，左、下、左下三个方向的位置均被计算出来，只能斜着遍历或反着遍历。
    for (i = n - 1; i >= 0; i--){
        for (let j = i + 1; j < n; j++){
            if (s[i] == s[j]){
                dp[i][j] = dp[i + 1][j - 1] + 2;
            } else{
                dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
            }
        }
    }
    return dp[0][n - 1];
}

动态规划的正则表达式

算法的设计是⼀个螺旋上升、逐步求精 的过程，绝不是⼀步到位就能写出正确算法。

写递归的技巧是管好当下，之后的事抛给递归

动态规划答疑篇

最优子结构

最优子结构：从子问题的最优结果能够推断出更大规模问题的最优结果；想要满足最优子结构，子问题之间必须相互独立。遇到这种最优子结构失效的情况，策略是改造问题。等价转化：最大分数差<=>最高分数和最低分数的差<=>求最高与最低分数。

最优子结构并不是动态规划独有的性质，但反过来，动态规划一定是要求的求最值的。动态规划就是通过base case一步步反推往上，只有符合最优子结构的问题才有发生这种链式反应的性质。

找寻最优子结构的过程其实就是证明状态转移方程正确性的过程，方程符合最优子结构就可以写暴力解了，写出暴力解就能看出有没有重叠子问题，有则优化。

dp数组的遍历方向

对dp数组的遍历方向有所困惑，可以正向、反向遍历，乃至斜向遍历；

1
2
3
4
5
6
//斜着遍历
for (let l = 2; l <= n; l++){
    for (let i = 0; i <= n - 1; i++){
        let j = l + i - 1;
    }
}

dp遍历设置的两大原则：1、遍历的过程中，所需的状态必须是已经计算出来的；2、遍历的终点必须是存储结果的那个位置；

即根据base case处于的位置来判断dp数组计算的起步，根据递推关系来判断dp数组递推的方向。

动态规划二维变一维

动态规划之股票买卖

题目：给定一个数组，它的第i个元素是一支给定的股票在第i天的价格，设计一个算法来计算你所能获取的最大利润，且你最多可以完成k笔交易。（你不能同时参与多笔交易，必须在再次购买之前出售）

穷举框架

这⾥，我们不⽤递归思想进⾏穷举，⽽是利⽤「状态」进⾏穷举。我们具 体到每⼀天，看看总共有⼏种可能的「状态」，再找出每个「状态」对应的 「选择」。我们要穷举所有「状态」，穷举的⽬的是根据对应的「选择」更 新状态。

⽐如说这个问题，每天都有三种「选择」：买⼊、卖出、⽆操作，我们⽤ buy, sell, rest 表⽰这三种选择。但问题是，并不是每天都可以任意选择这三 种选择的，因为 sell 必须在 buy 之后，buy 必须在 sell 之后。那么 rest 操作 还应该分两种状态，⼀种是 buy 之后的 rest（持有了股票），⼀种是 sell 之 后的 rest（没有持有股票）。⽽且别忘了，我们还有交易次数 k 的限制，就 是说你 buy 还只能在 k > 0 的前提下操作。

这个问题的「状态」有三个，第⼀个是天 数，第⼆个是允许交易的最⼤次数，第三个是当前的持有状态（即之前说的 rest 的状态，我们不妨⽤ 1 表⽰持有，0 表⽰没有持有）。然后我们⽤⼀个 三维数组就可以装下这⼏种状态的全部组合：

⽽且我们可以⽤⾃然语⾔描述出每⼀个状态的含义，⽐如说 dp[3][2][1] 的含义就是：今天是第三天，我现在⼿上持有着股票，⾄今最多进⾏ 2 次交 易。再⽐如 dp [2] [3] [0] 的含义：今天是第⼆天，我现在⼿上没有持有股 票，⾄今最多进⾏ 3 次交易。很容易理解，对吧？

我们想求的最终答案是 dp [n - 1] [K] [0]，即最后⼀天，最多允许 K 次交易， 最多获得多少利润。读者可能问为什么不是 dp[n - 1] [K] [1]？因为 [1] 代表⼿ 上还持有股票，[0] 表⽰⼿上的股票已经卖出去了，很显然后者得到的利润 ⼀定⼤于前者。

记住如何解释「状态」，⼀旦你觉得哪⾥不好理解，把它翻译成⾃然语⾔就 容易理解了。

状态转移框架

1
2
3
4
5
6
7
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]) 
max( 选择 rest , 选择 sell ) 
解释：今天我没有持有股票，有两种可能： 要么是我昨天就没有持有，然后今天选择 rest，所以我今天还是没有持有； 要么是我昨天持有股票，但是今天我 sell 了，所以我今天没有持有股票了。 

dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]) 
max( 选择 rest , 选择 buy ) 
解释：今天我持有着股票，有两种可能： 要么我昨天就持有着股票，然后今天选择 rest，所以我今天还持有着股票； 要么我昨天本没有持有，但今天我选择 buy，所以今天我就持有股票了

现在，我们已经完成了动态规划中最困难的⼀步：状态转移⽅程。如果之前 的内容你都可以理解，那么你已经可以秒杀所有问题了，只要套这个框架就 ⾏了。不过还差最后⼀点点，就是定义 base case，即最简单的情况

1
2
3
4
5
6
7
8
9
dp[-1][k][0] = 0 
解释：因为 i 是从 0 开始的，所以 i = -1 意味着还没有开始，这时候的利润当然是 0 。
dp[-1][k][1] = -infinity 
解释：还没开始的时候，是不可能持有股票的，⽤负⽆穷表⽰这种不可能。 
dp[i][0][0] = 0 
解释：因为 k 是从 1 开始的，所以 k = 0 意味着根本不允许交易，这时候利润当然是 0 。
dp[i][0][1] = -infinity 
解释：不允许交易的情况下，是不可能持有股票的，⽤负⽆穷表⽰这种不可能

总结一下：

1
2
3
4
5
6
7
base case:
    dp[-1][k][0] = dp[i][0][0]
    dp[-1][k][0] = dp[i][0][1] = -infinity
    
状态转移方程:
    dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
    dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])

k=1时

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
for (int i = 0; i < n; i++) { 
    if (i - 1 == -1){ 
        dp[i][0] = 0; 
        // 解释： 
        // dp[i][0] 
        // = max(dp[-1][0], dp[-1][1] + prices[i]) 
        // = max(0, -infinity + prices[i]) = 0 
        dp[i][1] = -prices[i]; 
        //解释： 
        // dp[i][1] 
        // = max(dp[-1][1], dp[-1][0] - prices[i]) 
        // = max(-infinity, 0 - prices[i]) 
        // = -prices[i] 
        continue; 
    }
    dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]); 
    dp[i][1] = Math.max(dp[i-1][1], -prices[i]); 
}
return dp[n - 1][0];

第⼀题就解决了，但是这样处理 base case 很⿇烦，⽽且注意⼀下状态转移 ⽅程，新状态只和相邻的⼀个状态有关，其实不⽤整个 dp 数组，只需要⼀ 个变量储存相邻的那个状态就⾜够了，这样可以把空间复杂度降到 O(1):

k= +infinity

k为正无穷，则可以把k、k-1看作一样，同样可以改写框架，数组中k已经不会改变，则不需要记录k。

1
2
3
4
5
6
7
8
9
10
int maxProfit_k_inf(int[] prices) {
    int n = prices.length; 
    int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE; 
    for (int i = 0; i < n; i++) { 
        int temp = dp_i_0; 
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]); 
        dp_i_1 = Math.max(dp_i_1, temp - prices[i]); 
    }
    return dp_i_0; 
}

k = infinity + coldDown

每次 sell 之后要等⼀天才能继续交易。只要把这个特点融⼊上⼀题的状态转 移⽅程即可： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]) ;
dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i]);
//解释：第 i 天选择 buy 的时候，要从 i-2 的状态转移，⽽不是 i-1 。
int maxProfit_with_cool(int[] prices) { 
    int n = prices.length; 
    int dp_i_0 = 0, dp_i_1 = Integer.MIN_VALUE; 
    int dp_pre_0 = 0; 
    // 代表 dp[i-2][0] 
    for (int i = 0; i < n; i++) { 
        int temp = dp_i_0; 
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]); 
        dp_i_1 = Math.max(dp_i_1, dp_pre_0 - prices[i]); 
        dp_pre_0 = temp; 
    }
    return dp_i_0; 
}

k = +infinity with fee

每次交易要⽀付⼿续费，只要把⼿续费从利润中减去即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]) ;
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i] - fee); 
//解释：相当于买⼊股票的价格升⾼了。 在第⼀个式⼦⾥减也是⼀样的，相当于卖出股票的价格减⼩了。
int maxProfit_with_fee(int[] prices, int fee) { 
    int n = prices.length; 
    int dp_i_0 = 0, 
    dp_i_1 = Integer.MIN_VALUE; 
    for (int i = 0; i < n; i++) { 
        int temp = dp_i_0; 
        dp_i_0 = Math.max(dp_i_0, dp_i_1 + prices[i]); 
        dp_i_1 = Math.max(dp_i_1, temp - prices[i] - fee); 
    }
    return dp_i_0; }

k = 2

k = 2 和前⾯题⽬的情况稍微不同，因为上⾯的情况都和 k 的关系不太⼤。 要么 k 是正⽆穷，状态转移和 k 没关系了；要么 k = 1，跟 k = 0 这个 base case 挨得近，最后也没有存在感。 这道题 k = 2 和后⾯要讲的 k 是任意正整数的情况中，对 k 的处理就凸显出 来了。

这道题由于没有消掉 k 的影响，所以必须要对 k 进⾏穷举：

1
2
3
4
5
6
7
8
9
10
11
12
int max_k = 2; 
int[][][] dp = new int[n][max_k + 1][2]; 
for (int i = 0; i < n; i++) { 
    for (int k = max_k; k >= 1; k--) { 
        if (i - 1 == -1) { 
            /*处理 base case */ 
        } 
        dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]); 
        dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]); 
    } 
}// 穷举了 n × max_k × 2 个状态，正确。 
return dp[n - 1][max_k][0];

k = any integer

有了上⼀题 k = 2 的铺垫，这题应该和上⼀题的第⼀个解法没啥区别。但是 出现了⼀个超内存的错误，原来是传⼊的 k 值会⾮常⼤，dp 数组太⼤了。 现在想想，交易次数 k 最多有多⼤呢？ ⼀次交易由买⼊和卖出构成，⾄少需要两天。所以说有效的限制 k 应该不超 过 n/2，如果超过，就没有约束作⽤了，相当于 k = +infinity。这种情况是之 前解决过的。 直接把之前的代码重⽤： 

1
2
3
4
5
6
7
8
9
10
11
12
int maxProfit_k_any(int max_k, int[] prices) { 
    int n = prices.length; 
    if (max_k > n / 2) 
        return maxProfit_k_inf(prices); 
    int[][][] dp = new int[n][max_k + 1][2]; 
    for (int i = 0; i < n; i++) 
        for (int k = max_k; k >= 1; k--) { 
            if (i - 1 == -1) { 
                /* 处理 base case */ 
            } 
            dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i0]); 
            dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices;

动态规划与回溯对比

题目：给定一个非负整数组，a1,a2,…an和一个目标数，S。现在你有两个符号+和-；对于数组中的任意一个整数，你都可以添加一个符号到前面，返回可以使最终数组和为目标数S的所有添加符号的方法数。

回溯思路

回溯算法就是一个暴力穷举算法；关键在于1、路径（即已经做出的选择），2、选择列表（当前可以做的选择），3、结束条件（到达决策树底层，无法再做选择的条件）。

1、路径：之前已经给前面的数字写出的正负号；2、选择列表：即每个数字可以选择给出正号或者负号；3、结束条件：即已经走到了最后一个数字；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
let result = 0;
//主函数
const findTargetSumWays = (nums, target) => {
    if (nums.length == 0) return 0;
    backtrack(nums, 0, target);
    return result
    
    const backtrack = (nums, i, rest){
        //base case
        if (i == nums.length){
            if (rest == 0){
                //说明恰好凑出target
                result++;
            }
            return;
        }
        //给nums[i]选择-号
        rest += nums[i];
        //递归来穷举nums[i+1]的可能性
        backtrack(nums, i + 1, rest);
        //撤销选择
        rest -= nums[i];
        
        //给nums[i]选择+号
        rest -= nums[i];
        //穷举nums[i+1]
        backtrack(nums, i + 1, rest);
        //撤销选择
        rest += nums[i];
    }
    
}

时间复杂度为O(2^N)，N为nums的大小，其实这个回溯算法就是个二叉树的遍历问题，树的高度就是nums的长度，故时间复杂度就是这棵二叉树的节点数，其实比较低效。

消除重叠子问题

动态规划快的原因就是消除了重叠子问题，关键在于看是否可能出现重复的状态；对于递归函数来说，函数参数中会变得参数就是状态，对于backtrack函数即i和rest。那么怎么一眼看出存在重叠子问题？

1、先抽象出算法得递归框架；

1
2
3
4
def dp(i, j):
    dp(i - 1, j - 1)#1
    dp(i, j - 1)#2
    dp(i - 1, j)#4

2、对于子问题dp(i-1, j-1)，如何通过原问题dp(i, j)来得到呢？有多种不同路径:比如dp(i,j)=>#1，和dp(i, j)=>#2 =>#3。一旦发现一条重复路径就说明存在巨量重复路径，也就是重叠子问题。

对于上题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
void backtrack(int i, int rest){
    backtrack(i + 1，rest - nums[i]);
    backtrack(i + 1, rest + nums[i]);
}
//当nums[i]=0时，出现两种状态完全相同得递归函数，这就是重叠子问题
//因此状态(i, rest)可以用备忘录来优化


const fingTargetSumWays = (nums, target) =>{
    if (nums.length == 0) return 0;
    return dp(nums, 0, target);
}

//备忘录
const memo = new Map();
const dp = (nums, i, rest) =>{
    //base case
    if (i == nums.length) {
        if (rest == 0) return 1;
        return 0;
    }
    //避免重复计算,转换成字符串从而作为Map的键来存储
    let key = i.toString() + "," + rest.toString；
    if (memo.has(key)) {
        return memo.get(key);
    }
    //还是穷举
    let result = dp(nums, i + 1, rest - nums[i]) + dp(nums, i + 1, rest + nums[i]);
    //这两种情况，"+"或者"-"号
    memo.set(key, result);
}

动态规划

上述的消除重叠子问题的方案，在最坏情况下的时间复杂度仍为O(2^N)，因为底层逻辑没变，暴力穷举，加上顺手进行了剪枝，提升了算法在某些情况的效率，但不算质的飞跃。其实，这个问题可以转化成一个子集划分的问题，而子集划分问题又是一个典型的背包问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
//我们把nums划分为两个子集A、B，分别代表分配+的数和分配-的数，则它们跟target存在如下关系：
sum(A) - sum(B) = target
sum(A) = target + sum(B)
sum(A) + sum(A) = target + sum(B) + sum(A)
2 * sum(A) = target + sum(nums)
//因此可以把问题转化为：nums中存在几个子集A，使得A中元素的和为(target + sum(nums)) / 2。
//这样就变成了经典的背包问题
//dp[i][j]代表前i个数构成结果为j的方法个数

const fingTargetSumWays = (nums, target) => {
    let sum = 0;
    for (let i = 0; i < nums.length; i++){
        sum += nums[i];
    }
    let len = nums.length;
    sum = (sum + target) / 2;
    let dp = new Array();
    //根据初始条件来初始化
    for (i = 0; i <= len + 1; i++) {
        dp[i] = new Array();
        for (let j = 0; j <= sum + 1; j++){
            dp[i][j] = 0;
        }
    }
    for (j = 0; j <= n; i++){
        dp[0][j] = 0;
    }
    //没有物品则没办法装背包，则为0
    for (i = 0; i <= n; i++){
        dp[i][0] = 1;
    }
    //背包的最大载重为0，则只有一种方法，即什么都不装
    
    for (i = 1; i <= nums.length; i++){
        for (j = 1; j <= sum; j++){
            if (j - nums[i - 1] < 0){
                //背包不足，不能装入第i个物品
                dp[i][j] = dp[i - 1] [j];
            } else {
                //装入或不装入的选择
                dp[i] [j] = dp[i - 1] [j] + dp[i - 1] [j - nums[i - 1]];
            }
        }
    }
    return dp[nums.length][sum];
}

总结一下：回溯算法虽好，但是复杂度很高，即使消除一些冗杂计算也只是剪枝，没有本质的改变；而动态规划则比较玄学，经过各种改造后，从一个加减法问题变成了子集问题，又变成背包问题，经过各种套路写出解法，还得使用状态压缩，加上反向遍历。

回溯算法框架

解决一个回溯问题，其实即使一个决策树的遍历过程，只需要思考3个问题，1、路径：就是已经做出的选择；2、选择列表：就是你当前可以做的选择；3、结束条件：到达决策树底层，无法再做选择的条件。

1
2
3
4
5
6
7
8
9
10
result = []
def backtrack(路径，选择列表)
    if 满足结束条件：
        result.add(路径)
        return
    
    for 选择 in 选择列表:
        做选择
        backtrack(路径，选择列表)
        撤销选择

核心其实就是for循环里面的递归，在递归调用前做选择，递归调用之后撤销选择。

回溯之全排列问题

穷举n个不重复数的全排列，求有多少个。

则可以画出该算法的决策树如下，每个节点都在做决策。[2]就是路径，记录你已经做过的选择；[1，3]是选择列表，表示当前可以做出的选择；[结束条件]就是遍历到树的底层，即选择列表为空的时候。

我们定义的backtrack函数其实就像一个指针，在这棵树上游走同时正确维护每个节点的属性，每当走到树的底层，其路径就是一个全排列。

全排列

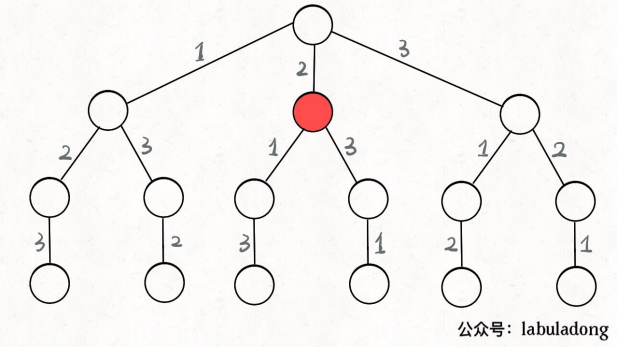
树的遍历问题：前序遍历、后序遍历。前序遍历代码在进入某一个节点之前的那个时间点执行，后序遍历代码在离开某个节点之后的那个时间点执行；函数在树上游走，正确维护其属性就是要在这两个特殊时间点搞动作。我们只要在递归之前做出选择，递归之后撤销选择，就能得到每个节点的选择列表、路径。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
List<List<Integer>> res = new LinkedList<>(); 
/* 主函数，输⼊⼀组不重复的数字，返回它们的全排列 */ 
List<List<Integer>> permute(int[] nums) { 
    // 记录「路径」 
    LinkedList<Integer> track = new LinkedList<>(); 
    backtrack(nums, track); 
    return res; 
}
// 路径：记录在 track 中 
// 选择列表：nums 中不存在于 track 的那些元素 
// 结束条件：nums 中的元素全都在 track 中出现 
void backtrack(int[] nums, LinkedList<Integer> track) { 
    // 触发结束条件 
    if (track.size() == nums.length) { 
        res.add(new LinkedList(track)); 
        return; 
    }
    for (int i = 0; i < nums.length; i++) { 
        // 排除不合法的选择 
        if (track.contains(nums[i])) 
            continue; 
        // 做选择 
        track.add(nums[i]); 
        // 进⼊下⼀层决策树 
        backtrack(nums, track); 
        // 取消选择
        track.removeLast(); 
    } 
}

我们这⾥稍微做了些变通，没有显式记录「选择列表」，⽽是通过 nums 和 track 推导出当前的选择列表：因为穷举整棵决策树是⽆法避免的。这也是回溯算法的⼀ 个特点，不像动态规划存在重叠⼦问题可以优化，回溯算法就是纯暴⼒穷*举，复杂度⼀般都很⾼。

回溯之N皇后问题

给你⼀个 N×N 的棋盘，让你放置 N 个 皇后，使得它们不能互相攻击。 这个问题本质上跟全排列问题差不多，决策树的每⼀层表⽰棋盘上的每⼀ ⾏；每个节点可以做出的选择是，在该⾏的任意⼀列放置⼀个皇后。

则可以直接套用框架：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
vector<vector<string>> res; 
/* 输⼊棋盘边⻓ n，返回所有合法的放置 */ 
vector<vector<string>> solveNQueens(int n) { 
    // '.' 表⽰空，'Q' 表⽰皇后，初始化空棋盘。 
    vector<string> board(n, string(n, '.')); 
    backtrack(board, 0); 
    return res; 
}

// 路径：board 中⼩于 row 的那些⾏都已经成功放置了皇后 
// 选择列表：第 row ⾏的所有列都是放置皇后的选择
// 结束条件：row 超过 board 的最后⼀⾏ 
void backtrack(vector<string>& board, int row) { 
    // 触发结束条件 
    if (row == board.size()) { 
        res.push_back(board); 
        return; 
    }
    int n = board[row].size(); 
    for (int col = 0; col < n; col++) { 
        // 排除不合法选择 
        if (!isValid(board, row, col)) 
            continue; 
        // 做选择 
        board[row][col] = 'Q'; 
        // 进⼊下⼀⾏决策 
        backtrack(board, row + 1); 
        // 撤销选择 
        board[row][col] = '.';
    }
}
//这部分的主要代码其实跟全排列差不多，都是遍历的思想，先检查是否合理，再进行决策并递归进下一层，下一层递归遍历完之后再撤销选择。
/* 是否可以在 board[row][col] 放置皇后？ */ 
bool isValid(vector<string>& board, int row, int col) { 
    int n = board.size(); 
    // 检查列是否有皇后互相冲突 
    for (int i = 0; i < n; i++) { 
        if (board[i][col] == 'Q') 
            return false; 
    }
    // 检查右上⽅是否有皇后互相冲突 
    for (int i = row - 1, j = col + 1; 
         i >= 0 && j < n; i--, j++) { 
        if (board[i][j] == 'Q') 
            return false; 
    }
    // 检查左上⽅是否有皇后互相冲突 
    for (int i = row - 1, j = col - 1; 
         i >= 0 && j >= 0; i--, j--) { 
        if (board[i][j] == 'Q') 
            return false; 
    }
    return true; 
}

函数 backtrack 依然像个在决策树上游⾛的指针，通过 row 和 col 就可 以表⽰函数遍历到的位置，通过 isValid 函数可以将不符合条件的情况剪枝：

这个问题的复杂度确实⾮常⾼，看看我们的决策树，虽 然有 isValid 函数剪枝，但是最坏时间复杂度仍然是 O(N^(N+1))，⽽且⽆ 法优化。如果 N = 10 的时候，计算就已经很耗时了。 有的时候，我们并不想得到所有合法的答案，只想要⼀个答案，怎么办呢其实特别简单，只要稍微修改⼀下回溯算法的代码即可：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 函数找到⼀个答案后就返回 
true bool backtrack(vector<string>& board, int row) { 
    // 触发结束条件 
    if (row == board.size()) { 
        res.push_back(board); 
        return true;
    }
    ...
    for (int col = 0; col < n; col++) {
        ... 
        board[row][col] = 'Q'; 
        if (backtrack(board, row + 1)) 
            return true; 
        board[row][col] = '.'; 
    }
    return false; 
}

回溯算法就是个多叉树的遍历问题，关键就是在前序遍历和后序遍历的位置 做⼀些操作，算法框架如下： 写 backtrack 函数时，需要维护⾛过的「路径」和当前可以做的「选择列 表」，当触发「结束条件」时，将「路径」记⼊结果集

动态规划的三个需要明确的点就是「状态」「选择」和 「base case」，是不是就对应着⾛过的「路径」，当前的「选择列表」和 「结束条件」某种程度上说，动态规划的暴⼒求解阶段就是回溯算法。只是有的问题具有 重叠⼦问题性质，可以⽤ dp table 或者备忘录优化，将递归树⼤幅剪枝，这 就变成了动态规划。⽽今天的两个问题，都没有重叠⼦问题，也就是回溯算 法问题了，复杂度⾮常⾼是不可避免的。

DFS与BFS详解

DFS的简要说明

(1)：深度优先搜索（Depth-First-Search）是搜索算法的一种。是沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所有边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。属于盲目搜索。

(2)：DFS是图论里面的一种搜索算法，他可以由一个根节点出发，遍历所有的子节点，进而把图中所有的可以构成树的集合都搜索一遍，达到全局搜索的目的。所以很多问题都可以用dfs来遍历每一种情况，从而得出最优解，但由于时间复杂度太高，我们也叫做暴力搜索。

(3)：DFS如同数据结构中的栈结构，是属于一种后进先出的结构，比如说一个羽毛球筒，把它装满之后，我们开始使用时，拿的总是最后放进去的那一个。所以这就导致了所有的点进入栈时有一个顺序，我们称之为 ：DFS序。

(4)：根据dfs的英文全写，我们可以知道这是一种深度优先搜索的搜索算法，什么叫做深度优先？意思就是它搜索一颗子树时，它要遍历到底才会 “回头” ，比如说：上有向图中的 搜索模式 为(以DFS序来描述)：a->b->e->b->f->c->f->b->c->b->a->c->a->d->g->d->a，有人就会问为什么搜索到c的时候不搜索a呢？因为我们假设的这是一个有向图。而且我们可以看到如果 你面对的图是一个 无向图，这个时候这个树将会持续搜索因为可能会形成环路，使得栈的结构一直进进出出，导致程序崩溃，所以我们也因该注意，在写DFS时，如果面对的是一个无向图的话我们需要进行标记。一般的标记方法有:①这个点的父节点被标记，使得子节点不能回到父节点造成循环②访问过的节点被标记。这两种方法视情况而定。

(5)：对于暴搜来说，因其复杂度太高，我们就会想去优化它的复杂度，这一过程称为剪枝，剪纸分为可行性剪枝和最优化剪枝，关于剪枝引申出一种名为记忆化搜索的方法，该方法与动态规划类似。

BFS简要说明

(1)：与DFS相对的那就是BFS了，BFS称为宽度优先搜索也叫做广度优先搜索，他是按层遍历每一种状态的下一种状态。

搞不懂？没关系我们来看一下一个例题：给你一个整数X，问是否存在一个这样一个数字A：①这个数字是X的倍数②这个数字仅由0与1这两种数字组成 例如 X=2，A=10。这个题当然可以用 DFS来做，我们以1为起点 这样就成了一个 0 1 二叉树，意思就是说每一种 情况 我们都可以 有两种选择 要么 添0，要么在后面 添1。所以我们可以写出代码：

1
2
3
4
5
6
7
8
9
10
void dfs(int start)
{
    if(A%X==0)//这是我们搜索结束的条件
    {
        ans=A;//让ans记录答案开始return
        return ans;
    }
    dfs(start*10);
    dfs(start*10+1);
}

所以我们开始试例子：输入 2按照dfs序的话，首先不符合条件，然后进入下一步搜索，X*10=10，发现10%2==0，然后开始返回ans记录A，这就是最后答案，但是你会发现程序崩溃了。
我们分析一下原因：DFS为深度优先搜索，所以我们的左子树可以看作是在末尾加0，然后右子树可以看作在末尾加1，所以这样就形成了一棵树。按照DFS我们的意图是让他搜索左子树，所以在左子树中找到了 满足条件的 数 ：10。但是为什么程序会崩溃呢？

(2）因为搜索到树之后，按照我们刚刚的DFS序，这个树遍开始回溯(你可以想象成这棵树开始回缩)，每回溯到一个节点，因为这个节点的 右子树还没有搜索，所以会再去搜索这个节点的右子树，但是这个节点的右子树是在末尾进行加1，而末尾是1绝对不可能是 2 的倍数 所以这个树会一直按照 往右子树 搜索的趋势 进行下去，导致程序崩溃。

1
2
3
4
5
6
7
8
9
10
11
//那是不是这个问题只能枚举了呢？其实DFS是可以的，在网络大神的果断判断之下这个问题出了一个新解：当搜索的深度为19时，此时的答案一定会出现，这时候回溯就好了。所以说我们加一个step记录深度就可以了：
void dfs(int start,int step)
{
    if(A%X==0&&step==19)//这是我们搜索结束的条件
    {
        ans=A;//让ans记录答案开始return
        return ans;
    }
    dfs(start*10,step+1);
    dfs(start*10+1,step+1);
}

(3)：还有没有更好的方法呢？在考虑这个问题的时候我们回顾一下刚刚为什么程序崩溃，原因就是因为DFS是一个深度优先搜索，他每次必须要 深搜到底 ，所以对于末尾是1来说永远没有结束条件所以它一直会搜索下去！这个时候我们可不可以想有没有这样一种搜索模式，出现A=10这个情况之后我们立刻停止就可以了呢？当然是有的，那就是BFS。

(4)：弄完上面这个例题，也就真正的引出了BFS也发现了DFS的一些小缺点。下面说一下上面留下的定义：按层遍历每一种的状态的下一种状态。首先BFS是与数据结构中的 队列 相似，队列是一种 先进先出的结构，这又比如说 你把一些水果按时间一天一个放进一个箱子里，但这些水果时间长了会变质，我们假设变质日期是一样的，那么你每次拿都是拿的最早放进去的那个。

所以说对于刚刚那个题目而言，我们如果按层遍历就不会出现程序崩溃的现象，比如说 第二层有10 11，那我们就不必搜索下一层了

DFS应用

(1).DFS由于有回溯的步骤，所以我们可以对其进行更新，比如并查集合并时的状态压缩都是使用DFS，还有图论中的 tarjan算法，lca等等。

(2)：搜索 有状态约束的 问题，比如说：N皇后问题；

BFS应用

(1)：求最短路，这个是图论里面的一种应用被称为SPFA算法，在我之前的博客中有总结过，所以在这里不再提。

(2)：求迷宫最短路，这种题目用DFS也是可以解的，用 DFS的思路:有许多条路可以到达终点我们求一下 到达终点的最小值。这样是非常耗时间的 而BFS不一样因为BFS是按层遍历，所以 每一层对于根节点来说距离一定是最小的，不需要再次更新，我们到达终点时这个距离一定一定是最小的，比如说：

（3)：同时移动性题目问题，火山在喷发，你在跑问是否可以跑出去。详情之前解释过这个问题：

(4)：倒水问题，每次倒水状态之间的转移，之前也有过例题：&&POJ341pots

(5)：路径还原，问从一个点到另一个点 的最短路径是多少，而题目不要求你输入最短距离，而是要求你还原路径这种时候通常需要加一个结构体数组来记录，其实上面的例题pots也是一个路径还原的问题，用一个简单的例题总结一下路径还原：

-------------本文结束感谢您的阅读-------------
坚持原创技术分享，您的支持将鼓励我继续创作！