Technical blog

IT小白的成长之旅

0%

发表于 分类于

前言

之前的项目在部署之后首屏加载过慢了，因此最近有想进行简单的优化一下，顺便就想以一个初学者的角度将项目优化的思路有条理的梳理一下，因为水平原因，很多方法可能只能写下思路，没办法应用在自己的项目上，而且可能很多的优化方案已经略有过时。主要还是想做一下有关优化知识的梳理吧，毕竟优化是一个永恒不变的话题。项目是基于vue框架开发的，但优化方法的思路是不拘泥于框架的。

代码层面优化

代码层面的优化这一部分其实比较杂乱，浅显的意思是要怎么去编写高性能点的代码？emm主要还是讲一下从一个新手的角度，避免出现一些影响性能的操作吧。

路由、模块懒加载

很常用的懒加载代码， 不用一次加载所有的路由或者模块，到需要引用时再进行加载，用函数来代替对象进行引入模块与路由，属于用vue框架时的基本操作吧。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//路由懒加载
export default new Router({
  routes: [
    {
      path: '/',
      name: 'HelloWorld',
      // 方法一：vue异步组件实现
      // component: resolve => (require(['@/components/HelloWorld'], resolve))
      // 方法二：import方法(常用)
      component: () => import('@/components/HelloWorld')
    }
  ]
})
//模块懒加载
export default {
  components: {
      // 方法一
    'HelloWorld': () => import('./HelloWorld'),
    // 方法二
    // HelloWorld': resolve => (['./HelloWorld'], resolve)
  }
}

图片懒加载

图片懒加载其实通常更多地应用于图片较多的网站，我自己的项目上由于图片比较少，就没有用到复杂的长屏懒加载。只是在图片或模块的ajax请求没有返回时，使用一个loading的特效来代替图片、组件进行填充，简单地实现了基础的懒加载？思路很简单：大概就是预设一个div的z-index，让其覆盖图片、组件的上面，默认为show。同时在ajax请求的异步回调上修改其CSS，变为hidden。elementUI等开源组件库上应该有类似的loading组件。

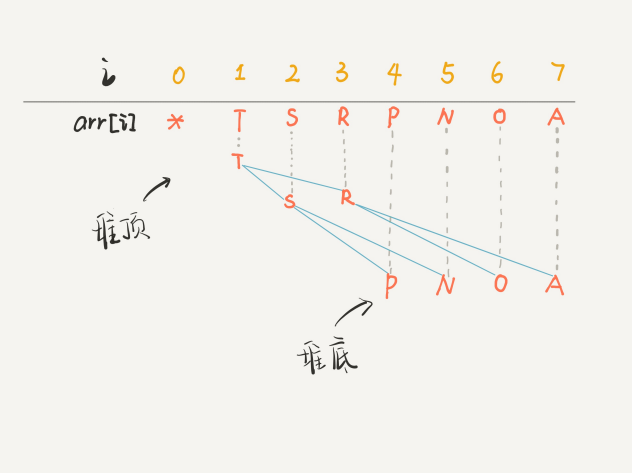
对于含有多图片的长页面，在你没有滚动到图片所在位置的页面中时，是用空的div来填充代替图片位置的。一旦我们通过滚动使得这个 div 出现在了可见范围内，那么 div 元素的内容就会发生变化，呈现其中的内容，这就是图片的懒加载。

下面我们简单实现下懒加载：其实该功能的关键在于获取两个值：1、当前可视区域的高度，通常用window.innerHeight 属性获取。

2、元素距离可视区域顶部的高度，我们这里选用 getBoundingClientRect() 方法来获取返回元素的大小及其相对于视口的位置。该方法的返回值是一个DOMRect。DOMRect 对象包含了一组用于描述边框的只读属性——left、top、right 和 bottom，单位为像素。除了 width 和 height 外的属性都是相对于视口的左上角位置而言的。其中top 属性代表了元素距离可视区域顶部的高度，正好用来实现功能。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
<!DOCTYPE html>
<html lang="en">
<head>
  <meta charset="UTF-8">
  <meta name="viewport" content="width=device-width, initial-scale=1.0">
  <meta http-equiv="X-UA-Compatible" content="ie=edge">
  <title>Lazy-Load</title>
  <style>
    .img {
      width: 200px;
      height:200px;
      background-color: gray;
    }
    .pic {
      // 必要的img样式
    }
  </style>
</head>
<body>
  <div class="container">
    <div class="img">
      // 注意我们并没有为它引入真实的src
      <img class="pic" alt="加载中" data-src="./images/1.png">
    </div>
    <div class="img">
      <img class="pic" alt="加载中" data-src="./images/2.png">
    </div>
    <div class="img">
      <img class="pic" alt="加载中" data-src="./images/3.png">
    </div>
    <div class="img">
      <img class="pic" alt="加载中" data-src="./images/4.png">
    </div>
    <div class="img">
      <img class="pic" alt="加载中" data-src="./images/5.png">
    </div>
     <div class="img">
      <img class="pic" alt="加载中" data-src="./images/6.png">
    </div>
     <div class="img">
      <img class="pic" alt="加载中" data-src="./images/7.png">
    </div>
     <div class="img">
      <img class="pic" alt="加载中" data-src="./images/8.png">
    </div>
     <div class="img">
      <img class="pic" alt="加载中" data-src="./images/9.png">
    </div>
     <div class="img">
      <img class="pic" alt="加载中" data-src="./images/10.png">
    </div>
  </div>
</body>
</html>
<script>
    // 获取所有的图片标签
    const imgs = document.getElementsByTagName('img')
    // 获取可视区域的高度
    const viewHeight = window.innerHeight || document.documentElement.clientHeight
    // num用于统计当前显示到了哪一张图片，避免每次都从第一张图片开始检查是否露出
    let num = 0
    function lazyload(){
        for(let i=num; i<imgs.length; i++) {
            // 用可视区域高度减去元素顶部距离可视区域顶部的高度
            let distance = viewHeight - imgs[i].getBoundingClientRect().top
            // 如果可视区域高度大于等于元素顶部距离可视区域顶部的高度，说明元素露出
            if(distance >= 0 ){
                // 给元素写入真实的src，展示图片
                imgs[i].src = imgs[i].getAttribute('data-src')
                // 前i张图片已经加载完毕，下次从第i+1张开始检查是否露出
                num = i + 1
            }
        }
    }
    // 监听Scroll事件
    window.addEventListener('scroll', lazyload, false);
</script>

ajax请求

现在项目中通常都不会去手写原生的ajax，毕竟因为异步的回调地狱嘛。我自己的项目用的是axios，定义如下：axios 是一个轻量的 HTTP客户端，它基于 XMLHttpRequest 服务来执行 HTTP 请求，支持丰富的配置，支持 Promise，支持浏览器端和 Node.js 端。但往往我们需要封装一下axios，毕竟如果每发起一次HTTP请求，就要把这些比如设置超时时间、设置请求头、根据项目环境判断使用哪个请求地址、错误处理等等操作都重写一遍就太麻烦了。这里贴一下我自己很简单的axios封装。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import Vue from 'vue'
import axios from 'axios'
var service = axios.create({
    baseURL: '',
    // http://qinghai.free.idcfengye.com/
    timeout:400000,
});
// 添加请求拦截器
service.interceptors.request.use(function (config) {
    // 在发送请求之前做些什么
    return config;
}, function (error) {
    // 对请求错误做些什么
    return Promise.reject(error);
});
// 添加响应拦截器
service.interceptors.response.use(function (response) {
    // 对响应数据做点什么
    return response;
}, function (error) {
    // 对响应错误做点什么
    return Promise.reject(error);
});

Vue.prototype.$http = service;
//挂载在vue的原型上，这样你后续在vue文件中使用this.$http便可以获取到service。

当然，这里ajax的优化其实并不是指简单的axios封装，毕竟这个属于常用操作。这个优化问题也是出自项目的主页，由于某些问题，主页中同一时间进行地ajax请求过多，一次跑过多的异步任务会导致页面的卡顿。开始时，我用的便是上述封装后的axios请求，为解决卡顿问题，开始时我希望能够使用fetch()来代替ajax请求，希望能达到目的；fetch()定义如下：

Fetch API是新的ajax解决方案 Fetch会返回Promise, fetch不是ajax的进一步封装，而是原生js，没有使用XMLHttpRequest对象。fetch(url, options).then()。

其实我感觉优点就三个：1、使用promise，这样也支持了async，编写异步时更加方便；2、可自定义是否携带cookie；3、fetch在ServiceWorker中使用。但实际项目中，ajax往往都被封装好了，例如上面的axios，这样前两项其实并没有所谓。但关键就在于第三项了。service work是基于web worker而来。

众所周知，javaScript 是单线程的，随着web业务的复杂化，开发者逐渐在js中做了许多耗费资源的运算过程，这使得单线程的弊端更加凹显。web worker正是基于此被创造出来，它是脱离在主线程之外的，我们可以将复杂耗费时间的事情交给web worker来做。但是web worker作为一个独立的线程，他的功能应当不仅于此。service work便是在web worker的基础上增加了离线缓存的能力。

特点：1、必须是https环境，本地调试localhost或者127.0.0.1环境也是可以的，2、依赖于cache api进行实现的3、依赖于h5的fetch Api；4、依赖于promise进行实现。但这里我自己并没有用这么复杂的优化方案，就不赘述了。

我自己运用基本的处理有：1、使用了axios对多并发请求的处理方案，当页面某个数据来源于多个互不关联的请求时，需要统一处理然后呈现。即使用axios.all(iterable)，参数：请求数组；axios.spread(callback)，参数： 对应请求返回值。API的应用实例如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
methods: {
  getAllTask() {
    return axios.get('/data.json', {
      params: {
        id: 10
      }
    })
  },
  getAllCity() {
    return axios.get('/city.json', {
      params: {
        id: 11
      }
    })
  }
},
mounted() {
  axios.all([this.getAllTask(), this.getAllCity()])
    .then(axios.spread(function(allTask, allCity) {
      console.log('请求1结果', allTask)
      console.log('请求2结果', allCity)
    }))
},

2、尽量复用ajax请求，当不同模块间可以公用同一接口的同一信息时，不要在两个模块中分别请求两次，而是尽量利用组件间通信来实现信息的共享；

2、设置HTTP缓存。HTTP 缓存是我们日常开发中最为熟悉的一种缓存机制。它又分为强缓存和协商缓存。

强缓存

优先级较高的是强缓存，在命中强缓存失败的情况下，才会走协商缓存。强缓存是利用 http 头中的 Expires 和 Cache-Control 两个字段来控制的。强缓存中，当请求再次发出时，浏览器会根据其中的 expires 和 cache-control 判断目标资源是否“命中”强缓存，若命中则直接从缓存中获取资源，不会再与服务端发生通信。

当服务器返回响应时，在 Response Headers 中将过期时间写入 expires 字段。接下来如果我们试图再次向服务器请求资源，浏览器就会先对比本地时间和 expires 的时间戳，如果本地时间小于 expires 设定的过期时间，那么就直接去缓存中取这个资源。expires写的是一个绝对的时间戳，例如：xxx年x月x日。而在 Cache-Control 中，我们通过 max-age字段 来控制资源的有效期。max-age 不是一个时间戳，而是一个时间长度。max-age 是一个相对时间，这就意味着它有能力规避掉 expires 可能会带来的时差问题。同样，因此cache-control的优先级比expires更高。Cache-Control 中还有更高优先级的s-maxage：用于表示 cache 服务器上（比如 cache CDN）的缓存的有效时间的，并只对 public 缓存有效。（public 与 private 是针对资源是否能够被代理服务缓存而存在的一组对立概念。）

协商缓存

协商缓存依赖于服务端与浏览器之间的通信。在协商缓存机制下，浏览器需要向服务器去询问缓存的相关信息，进而判断是重新发起请求、下载完整的响应，还是从本地获取缓存的资源。在该服务端提示缓存资源未改动（Not Modified），资源会被重定向到浏览器缓存，这种情况下网络请求对应的状态码是 304）。

实现：Last-Modified 到 Etag。Last-Modified 是一个时间戳，如果我们启用了协商缓存，它会在首次请求时随着 Response Headers 返回。随后我们每次请求时，会带上一个叫 If-Modified-Since 的时间戳字段，它的值正是上一次 response 返回给它的 last-modified 值。服务器接收到这个时间戳后，会比对该时间戳和资源在服务器上的最后修改时间是否一致，从而判断资源是否发生了变化。如果发生了变化，就会返回一个完整的响应内容，并在 Response Headers 中添加新的 Last-Modified 值；否则，返回如上图的 304 响应，Response Headers 不会再添加 Last-Modified 字段。

但是可能会有一个bug：我们编辑文件，但没有修改，服务器可能会以为我们修改了；修改文件的时间过快，服务器可能会感知不到。即：服务器并没有正确感知文件的变化。这样就引出了Etag，Etag 是由服务器为每个资源生成的唯一的标识字符串，这个标识字符串是基于文件内容编码的，只要文件内容不同，它们对应的 Etag 就是不同的。Etag 的生成过程需要服务器额外付出开销，会影响服务端的性能，这是它的弊端。同样，优先级方面，Etag高于Last-Modefied。

HTTP缓存决策流程：当我们的资源内容不可复用时，直接为 Cache-Control 设置 no-store，拒绝一切形式的缓存；否则考虑是否每次都需要向服务器进行缓存有效确认，如果需要，那么设 Cache-Control 的值为 no-cache；否则考虑该资源是否可以被代理服务器缓存，根据其结果决定是设置为 private 还是 public；然后考虑该资源的过期时间，设置对应的 max-age 和 s-maxage 值；最后，配置协商缓存需要用到的 Etag、Last-Modified 等参数。

组件库按需引入

这一点其实好理解，例如当你使用elementUI或者echarts这些组件库时，通常并没有用到其提供的全部组件，因此在import的时候，不需要全部引入整体，只需要引入你所用到的部分即可。

适用于V8引擎的JS代码

毫无疑问，就又是一个大坑了，关于对这个的理解我也是由他人的博客所看来的，不保证结论的正确性，只是记录下自己的了解。首先我们需要了解以下V8引擎底层的两个特征。

隐藏类

在V8引擎中采用了和动态查找完全不同的技术来实现属性的访问：动态地为对象创建隐藏类。每当一个新的属性被添加到对象中时，对象所对应的隐藏类会随之改变。乍一看似乎每次添加一个属性都创建一个新的隐藏类非常低效。实际上，利用类转移信息时，隐藏类可以被重用。即下次创建一个 Point 对象的时候，就可以直接共享由最初那个 Point 对象所创建出来的隐藏类。

这样的话，相当于一个构造函数中的所有属性都由一个隐藏类的链将他串联在了一起，由该构造函数新建的对象就可以直接共享该隐藏类链。主要的优点有：1、属性访问时不再需要从动态字典中进行查找了；2、为V8使用经典的基于类的优化和内联缓存技术提供了条件。

内联缓存技术：在第一次执行到访问某个对象的属性的代码时，V8会找出该对象的隐藏类；同时，V8会假设在相同的代码片段中其他所有的对象的属性访问都通过这一隐藏类来实现。只有在预测失败时，V8才会修改内联代码并移除刚才加入的内联优化。当有许多对象共享同一个隐藏类的时候，这样的实现方式下属性的访问速度可以接近大多数动态语言。使用内联缓存代码和隐藏类实现属性访问的方式和动态代码生成和优化的方式结合起来，即：你基于一个构造函数，构建多个实例时，用隐藏类的方法可以加快属性访问速度。

由隐藏得来的V8代码编写教训：1、在构造函数里初始化所有对象的成员(所以这些实例之后不会改变其隐藏类)；2、总是以相同的次序初始化对象成员；//可以更好利用隐藏类 3、永远不要delete对象的某个属性；4、方法：重复执行相同方法的代码将比仅执行一次的多个不同方法（由于内联缓存）的代码运行得更快。5、数组：避免稀疏数组

两次编译

V8有两个不同的运行时编译器：1、“完全”编译器（unoptimized）。一开始，所有的V8代码都运行在unoptimized状态。它的好处是编译速度非常快，它使代码初次执行速度非常快。2、“优化”编译器（optimized）。当V8发现某段代码执行非常热时，它会根据通常的执行路径进行代码优化，生成optimized代码。优化代码的执行速度非常快。

编译器有可能从“优化”状态退回到“完全”状态， 这就是deoptimized。这是很不幸的过程，优化后的代码没法正确执行，不得不退回到unoptimized版本。当然最不幸的是代码不停地被optimized，然后又被deoptimized， 这会带来很大的性能损耗，例如：for…in遍历对象的属性和try…catch中的代码会让编译器无法到达optimized状态。

使用教训：1、把for…in 内部的代码单独提出来作为函数，这样V8引擎就能对其进行优化；2、谨慎使用try..catch

闭包

闭包会使程序逻辑变复杂，有时会看不清楚是否对象内存被释放，因此要注意释放闭包中的大对象， 否则会引起内存泄露。谨慎使用闭包，有时候不当的闭包使用会造成大量的内存占用。

存储层面的优化

其实关于缓存方面上面的ajax请求里已经写了好多了，嗯，感觉布局有点问题，不过并不打算改了。这里就主要说说webpack打包方面的修改吧，毕竟算存储内容的优化？不过我是用vuecli构建的项目，其实该有的优化都已经默认配好了？就像tree-shaking？

在你使用vue-cli构建项目时，webpack的配置会被隐藏在vuecli的框架下面，不过想要自己进行特别的webpack配置也比较容易，根据vuecli官方网站的说明：调整 webpack 配置最简单的方式就是在 vue.config.js 中的 configureWebpack 选项提供一个对象：该对象将会被 webpack-merge 合并入最终的 webpack 配置。如果你需要基于环境有条件地配置行为，或者想要直接修改配置，那就换成一个函数 (该函数会在环境变量被设置之后懒执行)。该方法的第一个参数会收到已经解析好的配置。在函数内，你可以直接修改配置，或者返回一个将会被合并的对象。具体的配置方案因为我自己也不太懂，就不赘述了。

webpack-bundle-analyzer

如果你是使用vue-cli3构建的项目，则直接vue-cli-service build –report就会生成一个report.html，打开这个html就能看到webpack打包之后的模块与依赖的加载状态。如果不是由vuecli构建的项目，也很简单，直接npm install 安装webpack-bundle-analyzer模块，版本号过高的话可能有意外的错误，推荐安装5.0.0。之后在vue配置中引入该包，并自定义运行命令即可，具体的可参照官网。之后你就可以看到自己项目的打包分析了，针对那些用的比较少的模块，把全局引入修改成针对性引入、使用更轻量级的组件库。总之根据该打包分析图，尽量减少项目的体积即可。

gzip压缩

gzip压缩可以说是为了优化首屏加载速度最常用的方法之一了。Gzip 压缩背后的原理，是在一个文本文件中找出一些重复出现的字符串、临时替换它们，从而使整个文件变小。根据这个原理，文件中代码的重复率越高，那么压缩的效率就越高，使用 Gzip 的收益也就越大。反之亦然。主要的实现方法有两个：

1、项目正常打包部署，直接在服务端对nginx配置进行修改。这样设置时，当你请求时,服务端就会先将对应的文件压缩成.gz格式再发送给你，客户端接收到了.gz文件的格式之后再解压并执行后续操作。相当于用压缩的时间，换取了文件传输的时间，通常都会是正优化，除非项目体积过小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
http {
    include       mime.types;
    default_type  application/octet-stream;

    sendfile        on;
    #tcp_nopush     on;

    #keepalive_timeout  0;
    keepalive_timeout  65;

    # 开启gzip
    gzip  on;
    
    # 设置缓冲区大小
    gzip_buffers 4 16k;
    
    #压缩级别官网建议是6
    gzip_comp_level 6;
 
    #压缩的类型
    gzip_types text/plain application/javascript text/css application/xml text/javascript application/x-httpd-php;


    server {
        listen       8462;
        server_name  localhost;

        location / {
            root   dist;
            index  index.html index.htm;
        }

        error_page   500 502 503 504  /50x.html;
        location = /50x.html {
            root   html;
        }
    }
}

2、项目打包时对webpack进行特殊设置，安装插件（compression-webpack-plugin）；打包同时生成成两份文件，第一份为正常的文件，另一个为gz压缩后的文件，部署时将其全部部署至服务端。下面是vuecli构建项目的webpack配置参考，不用vuecli构建的，直接修改webpack配置即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
const CompressionPlugin = require('compression-webpack-plugin');
module.exports= {
    configureWebpack: {
        plugins: [
            new CompressionPlugin({
                algorithm: 'gzip', // 使用gzip压缩
                test: /\.js$|\.html$|\.css$/, // 匹配文件名
                filename: '[path].gz[query]', // 压缩后的文件名(保持原文件名，后缀加.gz)
                minRatio: 1, // 压缩率小于1才会压缩
                threshold: 10240, // 对超过10k的数据压缩
                deleteOriginalAssets: false, // 是否删除未压缩的源文件，谨慎设置，如果希望提供非gzip的资源，可不设置或者设置为false（比如删除打包后的gz后还可以加载到原始资源文件）
            })
        ],
    },
}

之后在nginx配置中使用：gzip_static on，该属性能够静态加载本地的gz文件，这样就完成了gzip。向较于上一种方案，这种方法虽然上传项目文件体积更大，但免去了服务端实时的压缩过程，速度会更快。

CDN缓存优化

定义：CDN （Content Delivery Network，即内容分发网络）指的是一组分布在各个地区的服务器。这些服务器存储着数据的副本，因此服务器可以根据哪些服务器与用户距离最近，来满足数据的请求。 CDN 提供快速服务，较少受高流量影响。相较于其他的缓存是为了优化网页流畅程度，CDN缓存更多的是为了优化首屏加载速度。

CDN 的核心点有两个，一个是缓存，一个是回源。这两个概念都非常好理解。“缓存”就是说我们把资源 copy 一份到 CDN 服务器上这个过程，“回源”就是说 CDN 发现自己没有这个资源（一般是缓存的数据过期了），转头向根服务器（或者它的上层服务器）去要这个资源的过程。

CDN 往往被用来存放静态资源。上文中我们举例所提到的“根服务器”本质上是业务服务器，它的核心任务在于生成动态页面或返回非纯静态页面，这两种过程都是需要计算的。业务服务器仿佛一个车间，车间里运转的机器轰鸣着为我们产出所需的资源；相比之下，CDN 服务器则像一个仓库，它只充当资源的“栖息地”和“搬运工”。

所谓“静态资源”，就是像 JS、CSS、图片等不需要业务服务器进行计算即得的资源。而“动态资源”，顾名思义是需要后端实时动态生成的资源，较为常见的就是 JSP、ASP 或者依赖服务端渲染得到的 HTML 页面。什么是“非纯静态资源”呢？它是指需要服务器在页面之外作额外计算的 HTML 页面。具体来说，当我打开某一网站之前，该网站需要通过权限认证等一系列手段确认我的身份、进而决定是否要把 HTML 页面呈现给我。这种情况下 HTML 确实是静态的，但它和业务服务器的操作耦合，我们把它丢到CDN 上显然是不合适的。

所以简单总结一下：静态资源走CDN便可以实现对静态资源加载的优化。同时静态资源往往并不需要 Cookie 携带什么认证信息，因此把静态资源和主页面置于不同的域名下，完美地避免了不必要的 Cookie 的出现。

理论的介绍大概就这么多了，在我自己的项目实践中，其实并没有把静态资源均部署在CDN上，毕竟技术力有限。只是将一些引入的公共框架代码，利用了BootCDN提供的免费资源进行取代。以本项目为例，我将vue、vuex、axios、echarts、elementUI均修改为CDN引入。主要的好处有两个：1、分离了公共库后，项目打包体积小了，打包速度提升了；2、使用CDN加载更加快速，且减轻了服务器压力。

具体实施步骤如下：1、在index.html中，添加CDN代码

1
2
3
4
5
6
7
8
9
10
11
12
13
...
<link href="https://cdn.bootcss.com/element-ui/2.7.2/theme-chalk/index.css" rel="stylesheet">
  </head>
  <body>
    <div id="app"></div>
    <script src="https://cdn.bootcdn.net/ajax/libs/vue/3.0.2/vue.cjs.js"></script>
    <script src="https://cdn.bootcdn.net/ajax/libs/vuex/4.0.0-rc.1/vuex.cjs.js"></script>
    <script src="https://cdn.bootcdn.net/ajax/libs/vue-router/3.4.8/vue-router.common.js"></script>
    <script src="https://cdn.bootcss.com/axios/0.18.0/axios.min.js"></script>
    <script src="https://cdn.bootcdn.net/ajax/libs/element-ui/2.15.0/index.js"></script>
    <script src="https://cdn.bootcdn.net/ajax/libs/vue-echarts/5.0.0-beta.0/vue-echarts.js"></script>
  </body>
</html>

2.在vue.config.js中加入webpack配置代码，关于webpack配置中的externals，请参考地址

渲染层面的优化

服务端渲染技术

提到渲染层面的优化就不得不说现在特别火的SSR技术了，其实它是一个相对的概念，其对立面是客户端渲染。客户端渲染就是常用的正常情况，服务端会把渲染需要的静态文件发送给客户端，客户端加载过来之后，自己在浏览器里跑一遍 JS，根据 JS 的运行结果，生成相应的 DOM。这种特性使得客户端渲染的源代码总是特别简洁。页面上呈现的内容，你在 html 源文件里里找不到——这正是它的特点。

服务端渲染的模式下，当用户第一次请求页面时，由服务器把需要的组件或页面渲染成 HTML 字符串，然后把它返回给客户端。客户端拿到手的，是可以直接渲染然后呈现给用户的 HTML 内容，不需要为了生成 DOM 内容自己再去跑一遍 JS 代码。使用服务端渲染的网站，可以说是“所见即所得”，页面上呈现的内容，我们在 html 源文件里也能找到。关于服务端渲染的实践方式，已经有nust.js这样的框架可以使用了，不过由于我自己的技术原因，并没有去实践一下这个新潮的技术。这里我就只说一下SSR的优缺点了，很多地方也都会提到这个。

优点：1、主要是出于效益的原因，因为SSR之后，搜索引擎以及各种爬虫才能够爬取网站的内容，这样才便于网站的推广。

2、服务端渲染解决了一个非常关键的性能问题——首屏加载速度过慢。在客户端渲染模式下，我们除了加载 HTML，还要等渲染所需的这部分 JS 加载完，之后还得把这部分 JS 在浏览器上再跑一遍。这一切都是发生在用户点击了我们的链接之后的事情，在这个过程结束之前，用户始终见不到我们网页的庐山真面目，也就是说用户一直在等！相比之下，服务端渲染模式下，服务器给到客户端的已经是一个直接可以拿来呈现给用户的网页，中间环节早在服务端就帮我们做掉了。

缺点：服务端渲染本质上是本该浏览器做的事情，分担给服务器去做。这样当资源抵达浏览器时，它呈现的速度就快了。乍一看好像很合理，但其实这样会成倍地增加服务端的压力，造成大量的成本，很有可能得不偿失。

CSS选择器优化

CSS 引擎查找样式表，对每条规则都按从右到左的顺序去匹配，与我们正常人的书写习惯刚好相反，因此在使用选择器时如果没有意识到这一点，就写出一些高性能消耗的选择器。例如: #mylist li {}。如果像这样写的话，浏览器必须遍历页面上每个 li 元素，并且每次都要去确认这个 li 元素的父元素 id 是不是 myList，这样会消耗大量性能。可以修改为：.myList_li {}同样，CSS中的通配符#会匹配所有元素，这样你使用时会让浏览器去遍历每一个元素。

以下为CSS书写时的性能提升方案：1、避免使用通配符，只对需要使用到的元素进行选择；2、关注可以通过继承实现的属性，避免重复匹配、重复定义；3、少使用标签选择器，尽量多使用类选择器。4、不要画蛇添足，id 和 class 选择器不应该被多余的标签选择器拖后腿。5、减少嵌套。后代选择器的开销是最高的，因此我们应该尽量将选择器的深度降到最低（最高不要超过三层），尽可能使用类来关联每一个标签元素。

DOM优化

减少回流与重绘

重绘不一定导致回流，回流一定会导致重绘。硬要比较的话，回流比重绘做的事情更多，带来的开销也更大。定义如下：

回流：当我们对 DOM 的修改引发了 DOM 几何尺寸的变化（比如修改元素的宽、高或隐藏元素等）时，浏览器需要重新计算元素的几何属性（其他元素的几何属性和位置也会因此受到影响），然后再将计算的结果绘制出来。这个过程就是回流（也叫重排）。

重绘：当我们对 DOM 的修改导致了样式的变化、却并未影响其几何属性（比如修改了颜色或背景色）时，浏览器不需重新计算元素的几何属性、直接为该元素绘制新的样式（跳过了上图所示的回流环节）。这个过程叫做重绘。

1、尽量多使用变量来进行缓存跟DOM相关的数据，避免引起DOM变化；

2、避免逐条改变样式，使用类名去合并样式；

3、将 DOM “离线”：当我们给元素设置 display: none，将其从页面上“拿掉”，那么我们的后续操作，将无法触发回流与重绘——这个将元素“拿掉”的操作，就叫做 DOM 离线化。拿掉一个元素，再将他放回去，虽然会触发一次回流，但在这期间对其做的任何操作，都不会太大影响性能。

减少获取DOM次数

在你需要多次操作并修改某个DOM时，只执行一次获取DOM的操作并将其存在变量中，这样就能节省获取DOM的性能消耗。

减少修改DOM的次数

对 DOM 的修改会引发渲染树的改变、进而去走一个（可能的）回流或重绘的过程。由于JS 的运行速度，比 DOM 快得多这个特性。我们减少 DOM 操作的核心思路，就是让 JS 去给 DOM 分压。这其实就是DOM Fragment](https://developer.mozilla.org/zh-CN/docs/Web/API/DocumentFragment) 的思路。

DocumentFragment 接口表示一个没有父级文件的最小文档对象。它被当做一个轻量版的 Document 使用，用于存储已排好版的或尚未打理好格式的XML片段。因为 DocumentFragment 不是真实 DOM 树的一部分，它的变化不会引起 DOM 树的重新渲染的操作（reflow），且不会导致性能等问题。

1
2
3
4
5
6
7
8
9
10
11
12
let container = document.getElementById('container')
// 创建一个DOM Fragment对象作为容器
let content = document.createDocumentFragment()
for(let count=0;count<10000;count++){
  // span此时可以通过DOM API去创建
  let oSpan = document.createElement("span")
  oSpan.innerHTML = '我是一个小测试'
  // 像操作真实DOM一样操作DOM Fragment对象
  content.appendChild(oSpan)
}
// 内容处理好了,最后再触发真实DOM的更改
container.appendChild(content)

DOM Fragment 对象允许我们像操作真实 DOM 一样去调用各种各样的 DOM API，我们的代码质量因此得到了保证。并且它的身份也非常纯粹：当我们试图将其 append 进真实 DOM 时，它会在乖乖交出自身缓存的所有后代节点后全身而退，完美地完成一个容器的使命，而不会出现在真实的 DOM 结构中。这种结构化、干净利落的特性，使得 DOM Fragment 作为经典的性能优化手段大受欢迎，这一点在 jQuery、Vue 等优秀前端框架的源码中均有体现。使用微任务队列，实现异步更新来避免过度渲染，就是用JS给DOM分压。

发表于 更新于 分类于

前言

项目是基于vue框架构建的，使用了elementUI组件库和echarts插件。开发过程中需要实现的一个需求是希望能够让首页实现大屏幕的适配效果。大概的完成思路借鉴了手机淘宝之前的flexible.js，就是获取不同屏幕的宽度，然后修改html根元素的字体大小；这样跟根元素字体大小绑定的rem就能够实时地监听屏幕的变化，实现不同屏幕的适配。

其实移动端的适配也是同理，不过好像有很多的坑，但本项目没有移动端适配的需求，因此就暂且采用了简单的rem适配的方法。由于首页中有echarts表单，需要也能够监听屏幕的变化，因此除了flexible.js以外，我们还需要自定义一个resize.js混入在首页的每个echarts上，让其也会实时跟踪监听屏幕变化，这样才能够实现首页所有元素的屏幕适配。

解决方案

基础定义

最简单最直接的方式就是直接用百分端来设置元素的尺寸；可以实现元素大小的自适应，但无法实现字体大小的自适应，而且尺寸转为百分比计算十分麻烦。其实我们需要的是一个和屏幕宽度正相关的单位，而且这个单位要和px很容易互相转化。这样我们就可以使用这种单位进行元素尺寸和字体大小的设置。

em单位为相对长度单位，是根据当前元素的父元素的字体大小来计算的；但父级元素改变时，则em会经常改变，因此后面推出了rem来代替em单位的功能。

rem单位也是一个相对长度单位，1rem等于html元素上字体设置的大小；我们只要设置html上font-size的大小就可以改变rem所代表的大小。

vw、vh都是viewport视窗的相对长度单位，100vw代表着viewport视窗的宽度，100vh代表着viewport视窗的高度。

设备像素比device pixel ratio简称dpr，即物理像素和设备独立像素的比值，设备像素比越大意味着你的手机屏幕越高清。

例如：电脑的dpr都为1，而iphone7的dpr为2，因此设计稿上的1px，要想让iphone7实现适配，CSS应该为0.5px。而有的浏览器在解析0.5px 的时候会把他解析成1px,所以呈现出来会变成2px。这就是经典的1px问题。

1px问题

解决方案：既然1个css像素代表两个物理像素，设备又不认0.5px的写法，那就画1px，然后再想尽各种办法将线宽减少一半。

1、图片大法及背景渐变。这两种方案原理一样,都是设置元素一半有颜色,一半透明,比如做一个2px高度的图片,其中1px是我们想要的颜色,1px设置为透明。

2、缩放大法。这也是flexible.js的解决方案，根据对应的dpr调整对应的缩放比例,从而达到适配的目的,直接缩放页面。

3、使用伪元素缩放。transform: scale(1, 0.5);实现缩放的功能。

flex弹性盒子布局

当我们采用flex布局时，flex会自己根据屏幕的宽度进行适配。关于flex适配的方案比较容易，通常跟rem一起来实现屏幕宽度不同时的界面适配。这里就只介绍一下flex的基础概念，具体的布局在理解定义后较为简单，就不列举实例了。

简要介绍下flex常用的属性：父容器：display:flex; flex-direction用于确定flex主轴布局的方向；接下来的 justify-content, align-items, align-content 用于确定 flex 项对于 flex 容器空间的空白如何处理。

flex容器中的子元素会成为flex项。flex属性是flex-grow, flex-shrink, flex-basis 三个属性的简写属性。grow、shrink分别代表着增长和收缩因子；basis代表着初始基准大小。默认值为：flex: 0 1 auto。flex-basis 指定固定的长度值时，其优先级高于width；flex-basis 指定百分比值时，其参考对象是 main size.所以其计算值 flex-basis: percent * mainSize px。

rem适配

原理其实前面已经讲过了，就是识别不同的屏幕长宽来设置不同的html根元素的字体大小，从而用动态的rem来实现界面的配置。关键在于如何识别不同的屏幕宽度。

1、利用媒体查询：@media screen and (min-width:XXX)来判断设备的尺寸，进而设置html的fontSize，比较麻烦且需要考虑较多。

2、利用js获取并设置fontSize，简单实例如下。以下代码是以iphone6为设计稿，结果是1rem=100px的实际像素，因为iphone6的设备像素比是2所以1rem在浏览器的预览中是50px，也就是实现了1rem和设备宽度成7.5倍的关系，设备宽度改变1rem的实际大小也会改变，

但我自己则是用了手机淘宝开源的flexible.js，稍微修改后便实现了需求，代码比这个实例复杂许多，具体代码会贴在文章的最后。

1
2
3
4
5
function setRem () {
        let htmlRem = document.documentElement.clientWidth
        document.documentElement.style.fontSize = htmlRem/7.5 + 'px'
      }
setRem()

3、使用vm、vh：vw、vh是新的一种相对单位是把可视区域分的宽高为100份类似于百分比布局，这种方案它不用去写js，不过兼容性有点差。

1
2
3
html{
    font-size: 10vw
}

px适配

根据不同的屏幕宽度，计算处不同的px值,所以当我们改变苹果的大小时,网站就会刷新动态计算出对应的px值,从而达到适配的目的。具体的实施代码没有找到，但其实原理逻辑相差不大。

项目实践

项目的适配大概有2部分吧：1、使用flexible.js来实现不同屏幕的适配；在基于vue框架的项目中，这里的flexible.js直接import进main.js即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175

(function(win, lib) {
  var doc = win.document;
  var docEl = doc.documentElement;
  var metaEl = doc.querySelector('meta[name="viewport"]');
  var flexibleEl = doc.querySelector('meta[name="flexible"]');
  var dpr = 0;
  var scale = 0;
  var tid;
  var flexible = lib.flexible || (lib.flexible = {});
  /*
  获取dom树：win.document.documentElement，后续向HTML插入dpr、font-size；
  分别取meta标签中元素，判断用户是否曾经设置过；viewport的meta标签，其主要用来告诉浏览器如何规范的渲染Web页面，而你则需要告诉它视窗有多大
   设备像素比简称为dpr，其定义了物理像素和设备独立像素的对应关系 = 物理像素 / 设备独立像素
   */

  if (metaEl) {
    console.warn("将根据已有的meta标签来设置缩放比例");
    var match = metaEl
      .getAttribute("content")
      // eslint-disable-next-line no-useless-escape
      .match(/initial\-scale=([\d\.]+)/);
    if (match) {
      scale = parseFloat(match[1]);
      dpr = parseInt(1 / scale);
    }
  } else if (flexibleEl) {
    var content = flexibleEl.getAttribute("content");
    if (content) {
      // eslint-disable-next-line no-useless-escape
      var initialDpr = content.match(/initial\-dpr=([\d\.]+)/);
      // eslint-disable-next-line no-useless-escape
      var maximumDpr = content.match(/maximum\-dpr=([\d\.]+)/);
      if (initialDpr) {
        dpr = parseFloat(initialDpr[1]);
        scale = parseFloat((1 / dpr).toFixed(2));
      }
      if (maximumDpr) {
        dpr = parseFloat(maximumDpr[1]);
        scale = parseFloat((1 / dpr).toFixed(2));
      }
    }
  }
  /*
   这段代码是判断你的meta标签里面是不是设置了name=viewport属性，如果你设置了viewport
   并且设置了initial-scale（初始屏幕的大小）我们将取到这个值作为dp
   */

  if (!dpr && !scale) {
    // eslint-disable-next-line no-unused-vars
    var isAndroid = win.navigator.appVersion.match(/android/gi);
    var isIPhone = win.navigator.appVersion.match(/iphone/gi);
    var devicePixelRatio = win.devicePixelRatio;
    if (isIPhone) {
      // iOS下，对于2和3的屏，用2倍的方案，其余的用1倍方案
      if (devicePixelRatio >= 3 && (!dpr || dpr >= 3)) {
        dpr = 3;
      } else if (devicePixelRatio >= 2 && (!dpr || dpr >= 2)) {
        dpr = 2;
      } else {
        dpr = 1;
      }
    } else {
      // 其他设备下，仍旧使用1倍的方案
      dpr = 1;
    }
    scale = 1 / dpr;
  }
  docEl.setAttribute("data-dpr", dpr);
  /*
  之后如果我们动态设置了scale或者设置了meta标签里面的name＝flexible的inital-scale，
  那么我们就根据自己设置的dpr在判断iphone手机的retina屏幕的dpr比值判断不同型号的倍数，最后我们在html上设置了data-dpr自定义属性。
  */

  if (!metaEl) {
    metaEl = doc.createElement("meta");
    metaEl.setAttribute("name", "viewport");
    metaEl.setAttribute(
      "content",
      "initial-scale=" +
        scale +
        ", maximum-scale=" +
        scale +
        ", minimum-scale=" +
        scale +
        ", user-scalable=no"
    );
    if (docEl.firstElementChild) {
      docEl.firstElementChild.appendChild(metaEl);
    } else {
      var wrap = doc.createElement("div");
      wrap.appendChild(metaEl);
      doc.write(wrap.innerHTML);
    }
  }
  /*
  之后当我们之前没有设置metaEl标签的话，那么需要我们手动的去创建meta标签，实现移动端的适配
  */

  function refreshRem() {
    var width = docEl.getBoundingClientRect().width;
    // 最小1366px，最大适配2560px
    if (width / dpr < 1366) {
      width = 1366 * dpr;
    } else if (width / dpr > 2560) {
      width = 2560 * dpr;
    }
    // 设置成24等份，设计稿时1920px的，这样1rem就是80px
    var rem = width / 24;
    docEl.style.fontSize = rem + "px";
    flexible.rem = win.rem = rem;
  }

  win.addEventListener(
    "resize",
    function() {
      clearTimeout(tid);
      tid = setTimeout(refreshRem, 300);
    },
    false
  );
  win.addEventListener(
    "pageshow",
    function(e) {
      if (e.persisted) {
        clearTimeout(tid);
        tid = setTimeout(refreshRem, 300);
      }
    },
    false
  );
  /*
  这段代码的目的就是监听window里面的resize和pageshow方法来实现css样式的重绘。
  函数里面就是实现取到当前设备的width之后根据width计算出rem的具体值，rem代表html的font-size，
  这里的rem代表的是一个自定义的rem，而不是rem属性！
  */

  if (doc.readyState === "complete") {
    doc.body.style.fontSize = 12 * dpr + "px";
  } else {
    doc.addEventListener(
      "DOMContentLoaded",
      // eslint-disable-next-line no-unused-vars
      function(e) {
        doc.body.style.fontSize = 12 * dpr + "px";
      },
      false
    );
  }
  /*
  之后我们判断document对象是否处于complete状态，
  如果完成状态我们给body一个font-size＝12*dpr的值，否则我们判断dom加载方法来实现body中的font-size的设置。
  这个设置是为了页面中字体的大小，而html中的font-size是为了设置页面的height，width等属性。
  */

  refreshRem();

  flexible.dpr = win.dpr = dpr;
  flexible.refreshRem = refreshRem;
  flexible.rem2px = function(d) {
    var val = parseFloat(d) * this.rem;
    if (typeof d === "string" && d.match(/rem$/)) {
      val += "px";
    }
    return val;
  };
  flexible.px2rem = function(d) {
    var val = parseFloat(d) / this.rem;
    if (typeof d === "string" && d.match(/px$/)) {
      val += "rem";
    }
    return val;
  };
})(window, window["lib"] || (window["lib"] = {}));

2、由于首页中还有echarts组件的展示，需要自定义一个函数来监听屏幕的变化，当屏幕变化时则修改echarts组件中chart的大小；这个resize的效果需要用防抖的函数来控制resize的频率。这里我把防抖写在了一个公共库里，就能方便复用，对于resize.js，直接混入在有echarts插件的vue文件中即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
export function debounce(func, wait, immediate) {
  let timeout, args, context, timestamp, result;

  const later = function() {
    // 据上一次触发时间间隔
    const last = +new Date() - timestamp;

    // 上次被包装函数被调用时间间隔 last 小于设定时间间隔 wait
    if (last < wait && last > 0) {
      timeout = setTimeout(later, wait - last);
    } else {
      timeout = null;
      // 如果设定为immediate===true，因为开始边界已经调用过了此处无需调用
      if (!immediate) {
        result = func.apply(context, args);
        if (!timeout) context = args = null;
      }
    }
  };

  return function(...args) {
    context = this;
    timestamp = +new Date();
    const callNow = immediate && !timeout;
    // 如果延时不存在，重新设定延时
    if (!timeout) timeout = setTimeout(later, wait);
    if (callNow) {
      result = func.apply(context, args);
      context = args = null;
    }

    return result;
  };
}

import { debounce } from '@/XXX/XXXX';
const resizeChartMethod = '$__resizeChartMethod';
export default {
  data() {
    // 在组件内部将图表init的引用映射到chart属性上
    return {
      chart: null,
    };
  },
  created() {
    window.addEventListener('resize', this[resizeChartMethod], false);
  },
  beforeDestroy() {
    window.removeEventListener('reisze', this[resizeChartMethod]);
  },
  methods: {
    // 通过lodash的防抖函数来控制resize的频率
    [resizeChartMethod]: debounce(function() {
      if (this.chart) {
        this.chart.resize();
      }
    }, 100),
  },
};

发表于 更新于 分类于

前言

如题，打算使用JS从头开始刷leetcode，大致地记录并讲解一下自己的解题思路吧，由于自己的水平原因，所以思路与解法都会比较偏新手向吧，同时不会只关注这一个题的思路，会有一些整体的思路与延伸吧。做这个记录的原因主要是想以新手的角度讲下自己解题遇到的弯路，同时也给自己加深印象吧。开始时可能注释会有些啰嗦，后续会减少不必要的代码解释。打算先写完并理解前150题吧，也并不打算分类的，因为前百题的思路都是经典解题思路，都需要慢慢体会吧。

1、两数之和

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 的那 两个整数，并返回它们的数组下标。你可以假设每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。你可以按任意顺序返回答案。转载自两数之和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number[]}
 */
const twoSum = (nums, target) => {
    let res = [];
    let map = new Map();
    for (let i = 0; i < nums.length; i++) {
        map.set(nums[i], i);
        //很简单的题目与逻辑，用map即哈希表的方法辅助查找即可，使用map的set方法构建。
    }
    for (let i = 0; i < nums.length; i++) {
        let newTarget = target - nums[i];
        if (map.has(newTarget) && (map.get(newTarget) !== i)) {
            res.push(i, map.get(newTarget));
            //使用has、get方法分别判断与获取索引
            //这里要注意下，不能两个相同索引相加
            return res;
        }
    }
}

2、两数相加

给你两个非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。请你将两个数相加，并以相同形式返回一个表示和的链表。你可以假设除了数字 0 之外，这两个数都不会以 0 开头。转载至两数之和

例：输入：l1 = [2,4,3], l2 = [5,6,4]；输出：[7,0,8]；解释：342 + 465 = 807。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */
/**
 * @param {ListNode} l1
 * @param {ListNode} l2
 * @return {ListNode}
 */
const addTwoNumbers = function(l1, l2) {
    let carry = 0;
    //定义进位，
    let sum = new ListNode(0);
    //一般链表题目的输出，需要先新建一个空的头节点，之后以该空结点作链表处理，从而能够避免因链表长度不够导致的报错,后续返回head.next
    let head = sum;
    while (l1 || l2 || carry) {
        let value1 = ((l1 === null) ? 0 : l1.val);
        //其实是在往前面补0，以确保两个加数位数一致
        let value2 = ((l2 === null) ? 0 : l2.val);
        sum.next = new ListNode((value1 + value2 + carry) % 10);
        carry = ((value1 + value2 + carry) >= 10 ? 1 : 0);
        sum = sum.next;
        if (l1) l1 = l1.next;
        if (l2) l2 = l2.next;
    }
    return head.next;
}

一般情况下，除了用链表来存储大数以外，在JS中更常用的是用字符串来保存，因此下面我们写一个字符串类型的大数相加，基本的逻辑和链表是一样的，主要是处理的方式不同，这里我就不再赘述原理了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
const add = function add(a, b){
  let m = "";
  let n = "";
  let res = [];
  let sum = 0;
  if (a.length > b.length){
    a = '0' + a;
    for (let i = b.length; i < a.length; i++){
      b = '0' + b;
    }
    m = a.split('');
    n = b.split('');
  } 
  else {
    b = '0' + b;
    for (let i = a.length; i < b.length; i++){
      a = '0' + a;
    }
    a = a.split('');
    b = b.split('');
}

  for (let i = a.length - 1; i >= 0; i--) {
    let k = (parseInt(a[i]) + parseInt(b[i]) + sum) % 10;
        res.unshift(k);
        if ((parseInt(a[i]) + parseInt(b[i]) + sum) >= 10) {
            if ((m === n) && (i = t)) {
                res.unshift("1");
            }
            sum = 1
        } else {
            sum = 0;
        }
  }
  let ans = res.join("");
  return ans;
}

3、无重复字符的最长子串

题目：给定一个字符串，请你找出其中不含有重复字符的 最长子串 的长度。

例如：输入: s = “abcabcbb”。输出: 3 。解释: 因为无重复字符的最长子串是 “abc”，所以其长度为 3。

思路：像这种子串的问题，最小覆盖子串、字符串的排列、找到字符串中所有字母异位词、无重复字符的最长子串。其实思路基本一致，子串的问题基本都能用滑动窗口的思想来解决。滑动窗口就是双指针的进阶版吧，即维护一个窗口，不断滑动并更新答案。

1、我们在字符串S中使用双指针中的左右指针技巧，初始化left = right = 0，把索引左闭右开区间[left, right)称为一个「窗口」。

2、我们先不断地增加right指针扩大窗口[left, right)，直到窗口中的字符串符合要求（包含了T中的所有字符）。

3、此时，我们停止增加right，转而不断增加left指针缩小窗口[left, right)，直到窗口中的字符串不再符合要求（不包含T中的所有字符了）。同时，每次增加left，我们都要更新一轮结果。

4、重复第 2 和第 3 步，直到right到达字符串S的尽头

第 2 步相当于在寻找一个「可行解」，然后第 3 步在优化这个「可行解」，最终找到最优解，也就是最短的覆盖子串。左右指针轮流前进，窗口大小增增减减，窗口不断向右滑动，这就是「滑动窗口」这个名字的来历。下面画图理解一下，needs和window相当于计数器，分别记录T中字符出现次数和「窗口」中的相应字符的出现次数。v

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
 * @param {string} s
 * @return {number}
 */
const lengthOfLongestSubstring = function(s) {
    let right = 0, left = 0;
    let length = 0;
    let arr = [];
    //本题的关键在于如何判断是否无重复子串，用indexOf判断新进项即可，或者直接用for循环判断
    while (right < s.length) {
        let index = arr.indexOf(s[right]);
        if (index !== -1) {
            arr.splice(0, index + 1);
            //将重复项之前全部删除,这里其实我们用字符串的操作来代替了滑动窗口的左移
        }
        arr.push(s[right]);
        length = Math.max(length, arr.length);
        right++;
    }
    return length;
};

4、寻找正序数组的两个中位数

题目：给定两个大小为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数。进阶：你能设计一个时间复杂度为 O(log (m+n)) 的算法解决此问题吗？

思路：暴力求解的话极其简单，直接for循环即可，第一时间会想到就是归并排序最后一步。按照 O(log (m+n)) 时间复杂度的话，面对有序数组的排序，首先想到二分查找，见下方，但是对于两个数组的二分查找该如何实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
function binary_search(arr,low, high, key) {
            if (low > high){
                return -1;
            }
            var mid = parseInt((high + low) / 2);
            if(arr[mid] == key){
                return mid;
            }else if (arr[mid] > key){
                high = mid - 1;
                return binary_search(arr, low, high, key);
            }else if (arr[mid] < key){
                low = mid + 1;
                return binary_search(arr, low, high, key);
            }
        };

该题的本质可扩展为寻找两个有序数组的第k小数，不一定是中位数，因此二分查找的本质是partition，每次都剔除k/2个数，且保证这些数都在第k小数左边，即都比第k小数小，然后k = k/2；递归处理后，得到第k小数。

二分查找，关键点在于要partition两个排好序的数组成左右两等份，partition需要满足len(Aleft)+len(Bleft)=(m+n+1)/2 - m是数组A的长度， n是数组B的长度并且partition后 A左边最大(maxLeftA), A右边最小（minRightA), B左边最大（maxLeftB), B右边最小（minRightB) 满足(maxLeftA <= minRightB && maxLeftB <= minRightA)有了这两个条件，那么median就在这四个数中，根据奇数或者是偶数。

奇数：median = max(maxLeftA, maxLeftB)；偶数：median = (max(maxLeftA, maxLeftB) + min(minRightA, minRightB)) / 2。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * 二分解法
 * @param {number[]} nums1
 * @param {number[]} nums2
 * @return {number}
 */
var findMedianSortedArrays = function(nums1, nums2) {
  // 确保nums1为更短的字符串
  if (nums1.length > nums2.length) {
    return findMedianSortedArrays(nums2, nums1);
  }
  const m = nums1.length
  const n = nums2.length
  let low = 0
  let high = m
  while(low <= high) {
    const i = low + Math.floor((high - low) / 2)
    const j = Math.floor((m + n + 1) / 2) - i

    const maxLeftA = i === 0 ? -Infinity : nums1[i-1]
    const minRightA = i === m ? Infinity : nums1[i]
    const maxLeftB = j === 0 ? -Infinity : nums2[j-1]
    const minRightB = j === n ? Infinity : nums2[j]

    if (maxLeftA <= minRightB && minRightA >= maxLeftB) {
      return (m + n) % 2 === 1
        ? Math.max(maxLeftA, maxLeftB)
        : (Math.max(maxLeftA, maxLeftB) + Math.min(minRightA, minRightB)) / 2
    } else if (maxLeftA > minRightB) {
      high = i - 1
    } else {
      low = low + 1
    }
  }
};

5、最长回文子串

题目：给你一个字符串 s，找到 s中最长的回文子串。

思路：最长回文子串的关键，其实通过双指针法也可以来处理，根据上题所述的思路很好进行解决，关键在于如何判定是否是回文子串的函数。但回文子串以及后序的回文子序列等问题，由于前后文联系比较紧密，且多次判断是否符合时间复杂度较大，通常使用动态规划来进行求解。

动态转移方程：dp[i] [j] = dp[i+1] [j-1] && (dp[i] === dp[j])；dp[i] [j]为true指的是：从i到j是回文串。

初始条件：即字符串长度仅为0、1时，必为回文子串，由于有这样的初始条件，初始项比较多，动态转移方程需要修改成:dp[i] [j] = (dp[i] === dp[j] && (j - i < 2 || dp[i+1] dp[j - 1]))。同样，由于初始条件必然有j > i，像这种初始条件的dp，一般都会使用斜向遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
 * @param {string} s
 * @return {string}
 */
const longestPalindrome = function(s) {
    let res = "";
    let dp = Array.from(new Array(s.length), () => new Array(s.length).fill(0));
    //利用Array.from构建二维数组，或者使用for循环也可
    for (let i = s.length - 1; i >= 0; i--) {
        //这里由于动态转移方程中dp[i][..]依赖于dp[i + 1][..]，因此需要倒着遍历来简化操作
        for (let j = i; j < s.length; j++) {
            //同样，由于初始条件原因，j从靠近i到远离i来遍历
            dp[i][j] = ((s[i] === s[j]) && (j - i < 2 || dp[i+1][j-1]));
            if (dp[i][j] && (j - i + 1 > res.length)) {
                res = s.substring(i, j+1);
                //substring截取字符串，包头不包尾
            }
        }
    }
    return res;
}

6、Z字形变换

题目：将一个给定字符串 s 根据给定的行数 numRows ，以从上往下、从左到右进行 Z 字形排列。比如输入字符串为 “PAYPALISHIRING” 行数为 3 时，排列如下：之后，你的输出需要从左往右逐行读取，产生出一个新的字符串，比如：”PAHNAPLSIIGYIR”。请你实现这个将字符串进行指定行数变换的函数：let convert(string s, int numRows)。

P A H N
A P L S I I G
Y I R

思路：关键在于找规律，中间列每列一个，且列数为numsRows-2；因此将一个第一列与后续的中间列作为一个循环，个数为numsRows + numsRows - 2。这样一个循环就能找出来了，再根据每个字符在循环中的位置，分别将其置入不同行。其中仅循环的第一位为第一行，V形排列。

1
2
3
4
5
6
7
8
9
10
11
12
13
const convert = function(s, numRows) {
    if (numRows === 1) {
        return s;
    }
    let rows = new Array(numRows).fill("");//用数组依次存储每一行的字符
    let circle = (2 * numRows - 2);
    for (let i = 0; i < s.length; i++) {
        let x = i % circle;
        rows[Math.min(x, circle - x)] += s[i];
    }
    let ans = rows.join("");
    return ans;
}

7、整数反转

题目：给出一个 32 位的有符号整数，你需要将这个整数中每位上的数字进行反转。

思路：在先判断正负号之后，用转字符串再转数组后，使用reverse()方法可以简单实现，但可以思考下用数学方法要如何处理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//先试一下数组反转，可以轻松解决
let reverse = function(x) {
    let res = x.toString().split("");
    if (res[0] == "-") {
        res.push("-");//反转后，相当于在前面加-，后面的负号parseInt会忽略掉
    }
    let ans = parseInt(res.reverse().join(""));
    if (ans >= Math.pow(2, 31) || ans <= -Math.pow(2, 31)) {
        ans = 0;
    }ue
    return ans;
}

//再试一下数学方法，关键在于一位位地取余数
let reverse = function(x) {
    let result = 0;
    while (x !== 0) {
        result = x % 10 + result * 10;
        x = (x / 10) | 0;
        //通过位运算符保证取整(无论正负)，同时强制转换为32位有符号整数
    }
    return (result | 0) === result ? result : 0;
    //result | 0 超过32位的整数转换结果不等于自身，可用作溢出判断。
}

8、字符串转整数

题目：请你来实现一个 atoi 函数，使其能将字符串转换成整数。

首先，该函数会根据需要丢弃无用的开头空格字符，直到寻找到第一个非空格的字符为止。接下来的转化规则如下：

如果第一个非空字符为正或者负号时，则将该符号与之后面尽可能多的连续数字字符组合起来，形成一个有符号整数。

假如第一个非空字符是数字，则直接将其与之后连续的数字字符组合起来，形成一个整数。

该字符串在有效的整数部分之后也可能会存在多余的字符，那么这些字符可以被忽略，它们对函数不应该造成影响。

假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时，则你的函数不需要进行转换，即无法进行有效转换。在任何情况下，若函数不能进行有效的转换时，请返回 0 。

注意：本题中的空白字符只包括空格字符 ‘ ‘ 。假设我们的环境只能存储 32 位大小的有符号整数。

1
2
3
4
5
6
7
8
9
10
11
//像这种字符串匹配的，先想到使用正则即可，先用trim来去掉前后的空格
/**
 * @param {string} s
 * @return {number}
 */
var myAtoi = function(s) {
    const re = new RegExp(/^(-|\+)?\d+/);
    let str = s.trim().match(re);
    let res = str ? Number(str[0]) : 0;
    return res >= 0 ? Math.min(res, 2**31 - 1) : Math.max(res, -(2**31))
};

9、回文数

题目：判断一个整数是否是回文数。回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。

思路：跟前面的整数反转一样，简单的思路的话，直接变数组之后，使用reverse()方法之后判断即可；同样也有数学方法来解决这个问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//直接用reverse()
/**
 * @param {number} x
 * @return {boolean}
 */
var isPalindrome = function(x) {
    return x === Number(x.toString().split('').reverse().join(''))
};

//利用数学方法来一步步求余
var isPalindrome = function(x) {
    if (x < 0) {
        return false;
    }
    let result = 0;
    let value = x;
    while (x !== 0) {
        result = result * 10 + x % 10;
        x = (x / 10) | 0;
    }
    if (value = result) {
        return true;
    } else {
        return false;
    }
}

10、正则表达式匹配

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
const isMatch = (s, p) => {
  if (s == null || p == null) return false;

  const sLen = s.length, pLen = p.length;

  const dp = new Array(sLen + 1);
  for (let i = 0; i < dp.length; i++) {
    dp[i] = new Array(pLen + 1).fill(false); // 将项默认为false
  }
  // base case
  dp[0][0] = true;
  for (let j = 1; j < pLen + 1; j++) {
    if (p[j - 1] == "*") dp[0][j] = dp[0][j - 2];
  }
  // 迭代
  for (let i = 1; i < sLen + 1; i++) {
    for (let j = 1; j < pLen + 1; j++) {

      if (s[i - 1] == p[j - 1] || p[j - 1] == ".") {
        dp[i][j] = dp[i - 1][j - 1];
      } else if (p[j - 1] == "*") {
        if (s[i - 1] == p[j - 2] || p[j - 2] == ".") {
          dp[i][j] = dp[i][j - 2] || dp[i - 1][j - 2] || dp[i - 1][j];
        } else {
          dp[i][j] = dp[i][j - 2];
        }
      }
    }
  }
  return dp[sLen][pLen]; // 长sLen的s串 是否匹配 长pLen的p串
};

11、盛水最多的容器

题目：给你 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。说明：你不能倾斜容器，且 n 的值至少为 2。

示例：输入：[1,8,6,2,5,4,8,3,7]；输出：49 ；解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

思路：其实是一个滑动窗口(双指针)类型的题目，暴力法：即穷举所有可能，分别计算面积并保存最大值。

双指针法：从左右两侧开始，将较矮柱子的指针进行移动，而先不移动高柱子的指针，原因：矮柱子选取后如果移动高柱子的话面积是一定会减小的，因为长度距离在变小的时候，此时高度只能小于或等于矮的柱子。因此只能移动矮的柱子这边才有可能使得高度比矮柱子大。所以，每次都移动的是高柱子的指针。这种方法其可以看作是暴力法的剪枝，而不是传统的滑动窗口。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * @param {number[]} height
 * @return {number}
 */
const maxArea = function(height) {
    let left = 0;
    let right = height.length - 1;
    let ans = 0;
    while (left < right) {
        let height1 = Math.min(height[left], height[right]);
        let aquare = height1 * (right - left);
        ans = Math.max(ans, aquare);
        if (height[left] < height[right]) {
            left++;
        } else {
            right--;
        }
    }
    return ans;
}

12、整数转罗马数字

思路：整数转罗马数字，比罗马数字转整数要简洁一些，同样关键在于求余的操作。

1
2
3
4
5
6
7
8
9
10
11
12
/**
 * @param {number} num
 * @return {string}
 */
var intToRoman = function(num) {
    var Q = ["", "M", "MM", "MMM"];
    var B = ["", "C", "CC", "CCC", "CD", "D", "DC", "DCC", "DCCC", "CM"];
    var S = ["", "X", "XX", "XXX", "XL", "L", "LX", "LXX", "LXXX", "XC"];
    var G = ["", "I", "II", "III", "IV", "V", "VI", "VII", "VIII", "IX"];
    return Q[Math.floor(num/1000)] + B[Math.floor((num%1000)/100)] + S[Math.floor((num%100)/10)] + G[num%10];
};
//利用Math.floor来直接取整数部分，而不是四舍五入

13、罗马数字转整数

思路：罗马数字转整数，首先将所有的组合可能性列出并添加到哈希表中

然后对字符串进行遍历，由于组合只有两种，一种是 1 个字符，一种是 2 个字符，其中 2 个字符优先于 1 个字符

先判断两个字符的组合在哈希表中是否存在，存在则将值取出加到结果 ans 中，并向后移2个字符。不存在则将判断当前 1 个字符是否存在，存在则将值取出加到结果 ans 中，并向后移 1 个字符，遍历结束返回结果 ans。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
const romanToInt = function(s) {
    const map = {
        I : 1,
        IV: 4,
        V: 5,
        IX: 9,
        X: 10,
        XL: 40,
        L: 50,
        XC: 90,
        C: 100,
        CD: 400,
        D: 500,
        CM: 900,
        M: 1000
    };
    let ans = 0;
    for(let i = 0;i < s.length;) {
        if(i + 1 < s.length && map[s.substring(i, i+2)]) {
            ans += map[s.substring(i, i+2)];
            i += 2;
        } else {
            ans += map[s.substring(i, i+1)];
            i ++;
        }
    }
    return ans;
};

14、最长公共前缀

题目：编写一个函数来查找字符串数组中的最长公共前缀。如果不存在公共前缀，返回空字符串 ""。

思路：很简单的题目，一个个的依次找最长公共前缀，先比较前两个，再用得出的公共前缀来匹配下一个；因此需要两层for循环，第一层，用于获取各个字符串，第二层对比每个字符串的各个字符。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * @param {string[]} strs
 * @return {string}
 */
var longestCommonPrefix = function(strs) {
    if (strs.length == 0) {
        return "";
    }
    let res = strs[0];
    for (let i = 1; i < strs.length; i++) {
        let compare = res;
        res = "";
        //前两个先比较,每次比较前修改compare,并重置res
        for (let j = 0; (j < strs[i].length) && (j < compare.length); j++) {
            if (strs[i][j] === compare[j]) {
                res = res + compare[j];
            } else {
                break;
            }
        }
        if (res == "") {
            return "";
        //提前退出的条件，剪枝j
        }
    }
    return res;
}

15、三数之和

给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有满足条件且不重复的三元组。注意：答案中不可以包含重复的三元组。

思路：关键在于如何保证不重复，用常规思路的话，先用三层for循环，之后再用哈希表去重；换一个思路，我们保持三重循环的大框架不变，只需要保证：第二重循环枚举到的元素不小于当前第一重循环枚举到的元素；第三重循环枚举到的元素不小于当前第二重循环枚举到的元素。即这样就只有一种顺序被枚举了，可以先排序，然后再查找。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
const threeSum = function(nums) {
    nums.sort((a, b) => {
        return (a - b);
    });
    let res = [];
    for (let i = 0; i < nums.length; i++) {
        if (nums[i] > 0) {
            break;
        }//在算法范畴上，进行逻辑的剪枝，此时后续不可能成立
        let target = -nums[i];
        if ((target + nums[i - 1] == 0) && i > 0) {
            continue;
            //从左往右遍历，此时遇到重复的则直接跳过，使用continue到for的下一个
        }
        //找到一个后，后续的使用双指针来遍历查找，同时去重
        let left = i + 1;
        let right = nums.length - 1;
        while (left < right) {
            let n2 = nums[left];
            let n3 = nums[right];
            if (n2 + n3 === target) {
                res.push([nums[i], n2, n3]);
                while (left < right && nums[left] === n2) left++;
                //去重复，后面有相同的则这里直接left++跳过去
                while (left < right && nums[right] === n3) right++;
                //这里在去重时，不要忘记基本的left < right
            } else if(n2 + n3 < target) {
                left++;
            } else {
                right--;
            }
        }
    }
    return res;
}

16、最接近的三数之和

题目：给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整数，使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。

思路：同样的思路，排序加双指针的做法能够很好地判断该如何去判断怎么去移动；同样，本题中不需要去考虑重复的问题了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
const threeSumClosest = function(nums, target) {
    nums.sort((a, b) => {
        return (a - b);
    });
    let ans = 0;
    let compare = Infinity;
    for (let i = 0; i < nums.length; i++) {
        let left = i + 1;
        let right = nums.length - 1;
        while (left < right) {
            let compare2 = target - nums[left] - nums[right] - nums[i];
            if (Math.abs(compare2) < compare) {
                ans = nums[i] + nums[right] + nums[left];
                compare = Math.abs(compare2)
            }
            if (compare2 < 0) {
                right--;
            } else {
                left++;
            }
        }
    }
    return ans;
}

17、电话号码的组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

思路：看上去十分容易，本质是一个三叉树的遍历方法，可以用BFS或者DFS。由这个题，我们可以先引申一下深度遍历和广度遍历的思路逻辑与基本方法。

1、DFS回溯（回溯是一种算法思想，一般可以用递归来实现。通俗点讲回溯就是一种试探,类似于穷举,但回溯有“剪枝”功能,）

回溯本质是暴力搜索，在问题的解空间树中，用 DFS 的方式，从根节点出发搜索整个解空间。如果要找出所有的解，则要搜索整个子树，如果只用找出一个解，则搜到一个解就可以结束搜索。类似「找出所有可能的组合」的问题，适合回溯算法。

回溯类题目，有三个关键点：

(1).选择:决定了你每个节点有哪些分支，可以帮助你构建出解的空间树。

(2).约束条件:用来剪枝，剪去不满足约束条件的子树，避免无效的搜索。

(3).目标:决定了何时捕获解，或者剪去得不到解的子树，提前回溯。

回溯法实质:它的求解过程实质上是先序遍历一棵“状态树”的过程。只不过，这棵树不是遍历前预先建立的，而是隐含在遍历过程中。如果认识到这点，很多问题的递归过程设计也就迎刃而解了。【回溯与递归的区别】回溯这个算法思想可以由递归这个算法结构来实现

我们构建一个递归来实现DFS，。递归的关键：递归关系与递归终止条件。（其他的扔给递归）

1、找整个递归的终止条件：递归应该在什么时候结束？2、找返回值：应该给下一级返回什么信息？3、本级递归应该做什么：在这一级递归中，应该完成什么任务？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
const letterCombinations = (digits) => {
    if (digits.length === 0) {
        return [];
    }
    const res = [];
    const map = new Map([['2','abc'], ['3','def'],['4','ghi'],['5','jkl'],['6','mno'],['7','pqrs'],['8','tuv'],['9','wxyz']]);

    const dfs = (curStr, i) => {//递归的传递参数包括，当前已经遍历树的结果、以及层数i
        if (i > digits.length - 1) {
            res.push(curStr);
            return;//一个树的递归分支结束
        }
        let letters = map.get(digits[i]);
        for (j of letters) {
            //for in 用于遍历对象,for of用于遍历有Iterator接口的对象,
            dfs(curStr, i+1);
        }
    }

    dfs("", 0);
    return res;
}

2、BFS广度搜索的方法

BFS通常是维护一个队列，即一层层地进行遍历，每次将对应层数的叶子加到之前层上，这里可以使用队列先进先出来解决，先进先出，依次地每次更新对应的下一层的结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * @param {string} digits
 * @return {string[]}
 */
const letterCombinations = (digits) => {
    if (digits.length == 0) {
        return [];
    }
    let res = [];
    let map = new Map([['2','abc'], ['3','def'],['4','ghi'],['5','jkl'],['6','mno'],['7','pqrs'],['8','tuv'],['9','wxyz']]);
    let queue = [];
    queue.push('');
    for (let i = 0; i < digits.length; i++) {//bfs二叉树的层数，就是digits的长度
        let levelSize = queue.length;//获取当前层的节点数，从而能逐个让当前层节点出列，更新接上对应后续节点后再依次入列
        for (let j = 0; j < levelSize; j++) {
            let curStr = queue.shift(); //模拟队列
            let letters = map.get(digits[i]);
            for (let k of letters) {
                queue.push(curStr + k);
            }
        }
    }
    return queue;
}

18、四数之和

题目：给定一个包含 n 个整数的数组 nums 和一个目标值 target，判断 nums 中是否存在四个元素 a，b，c 和 d ，使得 a + b + c + d 的值与 target 相等？找出所有满足条件且不重复的四元组

思路：其实跟前面的三数之和思路一样，后面两个数可以用双指针法来进行枚举；而前面两个数只能通过两层的for循环来实现。同样，先对数组进行排序，且添加每个数时都要进行重复判断。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
const fourSum = function(nums, target) {
    const quadruplets = [];
    if (nums.length < 4) {
        return quadruplets;
    }
    nums.sort((x, y) => x - y);
    const length = nums.length;
    for (let i = 0; i < length - 3; i++) {
        if (i > 0 && nums[i] === nums[i - 1]) {
            continue;//从左往右遍历，有跟上一条重复的则跳过
        }
        if (nums[i] + nums[i + 1] + nums[i + 2] + nums[i + 3] > target) {
            break;
        }
        if (nums[i] + nums[length - 3] + nums[length - 2] + nums[length - 1] < target) {
            continue;//上面两种情况都是剪枝，以减少事件复杂度
        }
        for (let j = i + 1; j < length - 2; j++) {
            if (j > i + 1 && nums[j] === nums[j - 1]) {
                continue;
            }
            if (nums[i] + nums[j] + nums[j + 1] + nums[j + 2] > target) {
                break;
            }
            if (nums[i] + nums[j] + nums[length - 2] + nums[length - 1] < target) {
                continue;
            }
            let left = j + 1, right = length - 1;
            while (left < right) {
                const sum = nums[i] + nums[j] + nums[left] + nums[right];
                if (sum === target) {
                    quadruplets.push([nums[i], nums[j], nums[left], nums[right]]);
                    while (left < right && nums[left] === nums[left + 1]) {
                        left++;
                    }
                    left++;
                    while (left < right && nums[right] === nums[right - 1]) {
                        right--;
                    }
                    right--;
                } else if (sum < target) {
                    left++;
                } else {
                    right--;
                }
            }
        }
    }
    return quadruplets;
};

19、删除链表的倒数第N个结点

题目:给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。进阶：你能尝试使用一趟扫描实现吗？

思路：不要求时间复杂度的话，先扫一遍来确定链表的长度，而后再根据长度找到倒数第N个结点；要使用一趟扫描实现的话，可以使用双指针来进行。第一个指针比第二个快n个，这样第二个指向尾节点时，则第一个指向要删除的结点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
const removeNthFromEnd = function(head, n) {
    let start = new ListNode;
    //一般先定义一个空结点放到现有的头节点前面，之后以该空结点作链表处理，从而能够避免因链表长度不够导致的报错
    start.next = head;
    let left = start;
    let right = start;
    for (let i = 0; i < n; i++) {
        right = right.next;
    }
    while (right.next != null) {
        left = left.next;
        right = right.next;
    }
    left.next = left.next.next;
    return start.next;
};

20、有效的括号

题目：给定一个只包括 ‘(‘，’)’，’{‘，’}’，’[‘，’]’ 的字符串，判断字符串是否有效。有效字符串需满足：左括号必须用相同类型的右括号闭合。左括号必须以正确的顺序闭合。注意空字符串可被认为是有效字符串。

思路：类似于栈的操作，判断很简单，这里就不赘述了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * @param {string} s
 * @return {boolean}
 */
/**
 * @param {string} s
 * @return {boolean}
 */
var isValid = function(s) {
    if (s.length == 0) {
        return true;
    }
    let compare = [];
    for (let i = 0; i < s.length; i++) {
        if (s[i] === "(" || s[i] === "[" || s[i] === "{") {
            compare.push(s[i]);
        }
        else if (s[i] === ")") {
            let a = compare.pop();
            if (a !== "(") {
                return false;
            }
        }
        else if (s[i] === "]") {
            let a = compare.pop();
            if (a !== "[") {
                return false;
            }
        }
        else if (s[i] === "}") {
            let a = compare.pop();
            if (a !== "{") {
                return false;
            }
        }
    }
    if (compare.length == 0) {
        return true;
    } else {
        return false;
    }
};

发表于 更新于 分类于

前言

正则表达式是匹配模式，要么匹配字符，要么匹配位置。关于正则表达式的原理和写法，网上的文章已经特别之多了，本篇文章将不着重于原理与方法，将直接以各种题目的形式来进行正则表达式的介绍，同样，题目的难度也将由弱至强。首先附上经典的正则链接网站：regulex。

基本符号

字符组 用于纵向模糊匹配，[]组内代表一个字符元素
^ 在第一位放脱字符，表示求反的概念
\d [0-9]，digit，表示一位数字
\D [^0-9]，表示除数字外的任意字符
\w [0-9a-zA-Z]，word，表示数字、大小写字母和下划线等单词字母
\W [^0-9a-zA-Z]，表示非单词字母
\s [\t\v\n\r\f]，space，表示空白格，包括空格、水平制表符、垂直制表符、换行符、回车符、换页符
\S [^ \t\v\n\r\f]，表示非空白符
. [^\n\r\u2028\u2029]，通配符，表示几乎任意字符，换行、回车、行分隔、段分隔符除外。
\1 反向引用，代表第一个用括号区分的分组，括号嵌套的号由开括号（来判断
量词 用于横向匹配，匹配多个字符，默认为贪婪匹配，可后加?变为惰性匹配
{m,} 表示至少出现m次
？ 等价于{0，1}，表示出现或不出现
+ 等价于{1，}，表示出现至少一次
* 等价于{0，}，表示出现任意次或者不出现
位置特性 用于位置方式的匹配
^、$ 脱字符、美元符号分别在多行匹配中，匹配行开头与行结尾
\b 匹配单词边界，具体就是\w与\W之间的位置，也包括\w与^、$之间的
\B 同样，是\b的反面的意思
(?=p) p为一个子模式，即匹配p前面的位置
(?!p) 其实就是(?=p)取反，除了p前面的位置以外的所有位置
方法 返回值与参数
test 一个在字符串中测试是否匹配的RegExp方法，它返回true或false。regex.test(string)
exec 一个在字符串中执行查找匹配的RegExp方法，它返回一个数组（未匹配到则返回null）regex.exec(string)
match 一个在字符串中执行查找匹配的String方法，它返回一个数组或者在未匹配到时返回null。string.match(regex)；match返回的是一个数组，包括各个括号匹配的内容
search 一个在字符串中测试匹配的String方法，它返回匹配到的位置索引，或者在失败时返回-1。
replace 个在字符串中执行查找匹配的String方法，并且使用替换字符串替换掉匹配到的子字符串。string.replace(regex, “ ”)
split 一个使用正则表达式或者一个固定字符串分隔一个字符串，并将分隔后的子字符串存储到数组中的String方法。

简单正则匹配

字符匹配

16进制颜色值

要求匹配：#12f3a1，#ffBabd，#FFF；等颜色值字母不区分大小写，且可为3位或者六位

1
2
3
let regex = /#([0-9a-fA-F]{6}|[0-9a-fA-F]{3})/g;
let string = "#12f3a1 #ffBabd #FFF #123 #586";
console.log(string.match(regex));

相当简单的正则，主要就是把基础知识运用下，只有两个分支匹配且逻辑清楚。

24小时时间

要求匹配：23：59，04：09，8：9，19：47；这样的时间，前面的0可以省略也可带着

1
2
3
4
5
6
7
8
let regex = /^(0?[0-9]|1[0-9]|2[0-3]):(0?[0-9]|[1-5][0-9])$/;
let arr = ["23:59", "04:09", "8,9", "19:47"];
let res = [];
for (let i = 0; i < arr.length; i++) {
    if (regex.test(arr[i])) {
        res.push(arr[i]);
    }
}

也是比较简单的正则，记得用括号将各段隔开，不然运算顺序可能不与你想的一致。

IP地址

要求匹配：192.168.225.255，156.234.156.215，1.2.3.4;类似的IP地址

1
2
3
4
5
6
7
8
let regex = /^(25[0-5]|2[0-4]\d|[0-1]\d{2}|[1-9]?\d)\.\1\.\1\.\1$/;
let arr = ["192.168.225.255", "156.234.156.215", "1.2.3.4"];
let res = [];
for (let i = 0; i < arr.length; i++) {
    if (regex.test(arr[i])) {
        res.push(arr[i]);
    }
}

这里的.字符需要转义，且利用括号分组来复用前面的正则。\1代表第一个括号引用的分组，根据第一个开括号(来确认。

带格式日期

要求匹配：2020-09-12，2043-12-30，2018/08/09，2016.06.21；分隔符有三种可用，且要求分隔符前后使用一样。

1
2
3
4
5
6
7
8
let regex = /\d{4}(-|\/|\.)\d{2}\1\d{2}/;
let res = [];
let arr = ["2020-09-12"，"2043-12-30"，"2018/08/09"，"2016.06.21"];
for (let i = 0; i < arr.length; i++) {
    if (regex.test(arr[i])) {
        res.push(arr[i]);
    }
}

要求分隔符前后一致，因此我们就必须用上题提过的括号分组复用，才能够实现这样的功能。我这里没有对日期的期限进行要求，直接用的数字均可，有要求的话，根据之前IP例题的逻辑，也能够很容易写出，这里就不再赘述。

同样，分组复用可以实现简单的替换，例如：想把yyyy-mm-dd替换成mm/dd/yyyy，以下的代码可以实现

1
2
3
4
5
6
let regex = /(\d{4})-(\d{2})-(\d{2})/;
let string = "2020-09-12";
let res = string.replace(regex, function() {
    return RegExp.$2 + "/" + RegExp.$3 + "/" + RegExp.$1;
});
//RegExp中的$1、$2、$3代表第1、2、3个分组

字符串去重

实例：将”aaaaabbbbbccccc”去重返回成为”abc”。利用括号分组的同样匹配，来实现查询出重复字符的效果，由于重复字符可以出现多次，因此后面还要加上+,表示至少出现一次。

1
2
3
4
let regex = /(\w)\1+/g;
//g代表全局匹配，会在一次匹配结束后继续匹配多次。而非仅匹配一次
let str = "aaaaabbbbbddddggggggggffff";
let res = str.replace(regex, "$1");

HTML标签

要求匹配HTML标签a内容，比如”“”“，即匹配出两个<>之间，且第一个字符为a

1
let regex = /<a[^>]+>/g

这里的^脱字符代表取反，即除了”>”以外均匹配。

驼峰字符串

要求将一个连续字符串如：get-element-by-id转化成驼峰形式

1
2
3
function toHump(str) {
    return str.replace(/-(\w)/g, function($1))
}

将-后面是字符的-与首字符的位置均匹配到，然后将$1，即-后的字符变成大写后replace进去

邮箱格式

1.不限制长度

2.不限制大小写

3.邮箱开头必须是数字或字符串

4.邮箱中可以使用字母、数字、点号、下划线、减号，但是不能连写点号、下划线、减号，如 abc_-de@q_.q.com

5.@符号前后不能为点号、下划线、减号

1
2
3
4
function isAvailableEmail(sEmail) {
    let reg = /^([\w+\._-])+@\w+[\.\w]+$/;
    return reg.test(sEmail);
}

识别十进制整数

修改 js 代码中 parseInt 的调用方式，使之通过全部测试用例。

eg：’12px’、’0x12’

1
2
3
4
5
6
7
8
9
function parse2Int(num) {
    var regex=/^\d+/;
    num=regex.exec(num)[0];
    return parseInt(num);
};
//或者可以直接使用parseInt(num, 10)；这个API会自动识别非十进制的数，将其排除在外
function parse2Int(num) {
    return parseInt(num,10);
}

颜色字符串转换

考的知识点两个：

  1. 正则表达式匹配；

  2. toString(16)转换进制；toString()可用于转换进制、判断引用类型。

做的过程中注意：

  1. 数值超界（0-255）
  2. 不足两位补零
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
function rgb2hex(sRGB) {
    let reg = /rgb\((\d+),\s*(\d+),\s*(\d+)\)/;
    let res = sRGB.match(reg);//match返回一个数组或者在未匹配到时返回null
    if (!res) {
        return sRGB;
    } else {
        let str = '#';
        for (let i = 1; i <= 3; i++) {
            let num = parseInt(res[i]);
            if (num <= 255 && num >= 0) {
                str += (num < 16 ? '0' + num.toString(16) : num.toString(16));
            } else {
                return sRGB;
            }
        }
        return str;
    }
}

变为驼峰

replace() 方法返回一个由替换值（replacement）替换一些或所有匹配的模式（pattern）后的新字符串。

这个用法的本质就是：对str使用RegArg做match()匹配，如果匹配到多项结果（比如使用了全局匹配g，或者分组），那么每一个匹配结果都将执行一次FuncArg函数，并且用该函数的返回值替代源字符串中的匹配项。

第一个参数可以是字符串或正则表达式，如果提供的是字符串，只会替换第一个子字符串。如果想替换所有子字符串，需要提供一个指定了 g 的正则表达式。

第二个参数可以是字符串或函数。如果是字符串，可以使用一些特殊的 字符序列：

如果第二个参数也可以是函数，这个函数接收多个参数：function (match[，p1, p2, …, pn], offset, string)

  • match：匹配的子串，等同于前面提到的 $&
  • p1-p2：为捕获组对应的匹配字符串（如果设置了捕获组）。
  • offset：模式匹配项位于输入字符串的位置
  • string：输入的原始字符串。
  • 函数的返回值：返回值即为替换的文本。

css 中经常有类似 background-image 这种通过 - 连接的字符，通过 javascript 设置样式的时候需要将这种样式转换成 backgroundImage 驼峰格式，请完成此转换功能

1、以 - 为分隔符，将第二个起的非空单词首字母转为大写

2、-webkit-border-image 转换后的结果为 webkitBorderImage

1
2
3
4
5
6
7
8
9
function cssStyle2DomStyle(sName) {
    let reg = /-(\w)/g;
    let res = sName.replace(reg, function(fullMatch, g1, index) {
        if (index === 0) return g1;
        //当模式串匹配的为单词的首项时，证明-在最前面，此时返回小写字母，将-a替换成a。
        return g1.toUpperCase();
    });
    return res;
}

获取url中参数

  1. 指定参数名称，返回该参数的值 或者 空字符串

  2. 不指定参数名称，返回全部的参数对象 或者 {}

  3. 如果存在多个同名参数，则返回数组

例:输入：http://www.nowcoder.com?key=1&key=2&key=3&test=4#hehe key；输出：[1, 2, 3]

方法一：使用字符串拼接来匹配。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/*  获取URl中的参数
* @para url 
* @para key 参数名*/
function getUrlParam(sUrl, sKey) {
    var left= sUrl.indexOf("?") + 1
    var right= sUrl.lastIndexOf("#")
    var parasString = sUrl.slice(left, right)
    var paras = parasString.split('&');
    var parasjson = {}
    paras.forEach(function (value, index, arr) {
        var a = value.split('=');
        parasjson[a[0]] !== undefined ? parasjson[a[0]] = [].concat(parasjson[a[0]], a[1]) : parasjson[a[0]] = a[1];
    });

    let result = arguments[1] !== void 0 ? (parasjson[arguments[1]] || '') : parasjson;
    return result
}

方法二：使用正则中的replace进行替换

1
2
3
4
5
6
7
8
9
function getUrlParam2(sUrl, sKey) {
    var result, Oparam = {};
    sUrl.replace(/[\?&]?(\w+)=(\w+)/g, function ($0, $1, $2) 
        console.log('$0:' + $0 + "     $1:" + $1 + "     $2:" + $2);
        Oparam[$1] === void 0 ? Oparam[$1] = $2 : Oparam[$1] = [].concat(Oparam[$1], $2);
    });
    sKey === void 0 || sKey === '' ? result = Oparam : result = Oparam[sKey] || '';
    return result;
}

方法三：使用正则中的exec方法

1
2
3
4
5
6
7
8
9
10
11
function getUrlParam3(sUrl, sKey) {
    var resObj = {};
    var reg = /(\w+)=(\w+)/g;
    while (reg.exec(sUrl)) {
        resObj[RegExp.$1] ? resObj[RegExp.$1] = [].concat(resObj[RegExp.$1], RegExp.$2) : resObj[RegExp.$1] = RegExp.$2;
    }
    if (sKey) {
        return (resObj[sKey] ? resObj[sKey] : '');
    }
    return resObj;
}

域名解析

函数parseUrl实现将一段url字段解析为Object，例如url为：”http://www.xiyanghui.com/product/list?id=123456&sort=discount#title";parseUrl(url)返回的结果为object如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
let object = {
    protocol:"http",
    host:"www.xiyanghui.com",
    path:"product/list",
    query: {
        id:"123456",
        sort:"discount"
    },
    hash:"title"
}

function parseUrl(str) {
    // 判断是否传入参数
    if (str) {
        var obj = {};
        var queryArr = [];
        // 正则表达式规则
        var re = /^(http[s]?):\/\/([0-9a-zA-Z\.]+)\/([a-zA-Z0-9\/]+)\?([a-zA-Z0-9\=\&]+)#([0-9a-zA-Z\.]+)$/;
        // 利用正则表达式将字符串分组
        var reArr = re.exec(str);
        if (reArr) {
            obj.peotocol = reArr[1];
            obj.host = reArr[2];
            obj.path = reArr[3];
            queryArr = reArr[4].split(/[\&\=]+/);
            obj.query = {};
            for (var i = 0; i < queryArr.length; i += 2) {
                obj.query[queryArr[i]] = queryArr[i + 1];
            }
            obj.hash = reArr[5]
            return obj;
        } else {
            return null;
        }
    } else {
        return null;
    }
}

位置匹配

千位分隔符

千位分隔符的关键在于两点：1、使用量词+多次匹配d{3}；2、要求匹配的位置不能是开头，因此用(?!^)

1
2
3
4
let regex = /(?!^)(?=(\d{3})+$)/g;
let regex = /(?!^)(?=(\d{3})+$)/g;//先要求匹配的位置不能是开头,$代表从单词末尾开始匹配，/g代表
let string = "123456789";
let res = string.replace(regex, ',');

如果还要求支持”12345783 23498237489 3219482”这样多个数字间用空格来区分的输入的话，只需要将^、$进行修改，改成\b，从而匹配多个连续字符的开头、结尾，而不是匹配整个字符串的开头、结尾。

1
2
3
let regex = /(?!\b)(?=(\d{3})+\b)/g;
let string = "12345783   23498237489  3219482";
let res = string.replace(regex, ',');

密码判断

多种条件的密码判断往往写成多个小的正则进行判断，下面基本使用三个小的条件进行密码判断。总的要求是：密码长度6-12位，由数字、小写字符、大写字符组成，但必须至少包括2种字符，且必须包含数字

1
2
3
4
5
6
7
8
9
10
11
12
13
//1、要求密码长度6-12位
let regex1 = /^[0-9A-Za-z]{6,12}$/;
//2、要求必须包含数字
let regex2 = /?=.*[0-9]/;//即任意数量任意字符的后面前一个位置，后面会接一个数字=>包含一个数字
//3、要求同时包含两种
let regex3 = /(?=.*[0-9])(?=.*[a-z])/;
let arr = ["192.168.225.255", "156.234.156.215", "1.2.3.4"];
let res = [];
for (let i = 0; i < arr.length; i++) {
    if (regex1.test(arr[i]) && regex2.test(arr[i]) && regex3.test(arr[i])) {
        res.push(arr[i]);
    }
}

替代正则

并不是所有的问题均适合使用正则解决：1、有些看似简单的问题，但正则做不到；2、有些能用字符串简单API就能解决的问题，使用正则会提高时间负杂度。

提取年月日

1
2
3
4
5
6
7
8
9
10
11
12
let string = "2020-09-01";
let regex = /^(\d{4})-(\d{2})-(\d{2})/;
console.log(string.match(regex));
//输出为["2020-09-01", "2020", "09", "01", index: 0, input: "2020-09-01"]

//其实，用字符串的split方法来做即可：
let string = "2020-09-01";
let res = string.split("-");
console.log(res);//输出为["2017", "07", "01"]
/*split()方法用于把一个字符串分割成字符串数组。
separator    必需。字符串或正则表达式，从该参数指定的地方分割 stringObject。
howmany    可选。该参数可指定返回的数组的最大长度。如果设置了该参数，返回的子串不会多于这个参数指定的数组。如果没有设置该参数，整个字符串都会被分割，不考虑它的长度。*/

模糊查询

需要实现的功能是类似百度搜索框的模糊查询，这里先只考虑JS代码，构建的函数传入参数有2个，分别是list存储所有关键词信息的数组、keyword模糊查询的关键词、res查询得出的结果。

indexOf方法

stringObject.indexOf(searchValue)该方法从头到尾检索字符串stringObject，看它是否含有子串searchValue，开始检索得位置在字符串的开头，找到searchValue时，则返回其第一次出现的位置，没有找到则返回-1。

1
2
3
4
5
6
7
8
9
function fuzzyQuery (list, keyWord) {
    let res = [];
    for (let i = 0; i < list.length; i++) {
        if (list[i].indexOf(keyWord) >= 0) {
            res.push(list[i]);
        }
    }
    return res;
}

split方法

stringObject.split(separator)。该方法通过在separator指定的边界处将字符串stringObject分割成子串并返回子串数组。返回的数组中的字串不包括separator自身。如果stringObject中不存在separator，将返回一个只包含stringObject的数组。故可以根据返回数组的长度来判断是否存在子字符串separator

1
2
3
4
5
6
7
8
9
function fuzzyQuery(list, keyWord) {
    let res = [];
    for (let i = 0; i < list.length; i++) {
        if (list[i].split(keyWord).length > 1) {
            res.push(list[i]);
        }
    }
    return res;
}

match方法

该方法在字符串内检索指定的值，或找到一个或多个正则表达式的匹配；如果没有找到任何匹配的文本，将返回null。否则，将返回一个数组。

1
2
3
4
5
6
7
8
9
function fuzzyQuery(list, keyWord) {
    let res = [];
    for (let i = 0; i < list.length; i++) {
        if (list[i].match(keyWord) != null) {
            res.push(list[i]);
        }
    }
    return res;
}

test方法

1
2
3
4
5
6
7
8
9
10
function fuzzyQuery(list, keyWord) {
    let reg = new RegExp(keyWord);
    let res = [];
    for (let i = 0; i < list.length; i++) {
        if (reg.test(list[i])) {
            res.push(list[i]);
        }
    }
    return res;
}

搜索框模糊查询实现

简单html实现

主要关注html实现，就不用上述定义的函数了，而是用更简单的方式。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
<!DOCTYPE html>
<html>
<head>
<meta http-equiv="Content-Type" content="text/html; charset=utf-8"/>
<title></title>
<script type="text/javascript">
onload = function () {
    //onload事件，页面在加载完成时马上执行的一组代码
    function handle() {
        var keyWords = { 
            "a": ["abada", "asdkasdfda", "askfdlf"],
            "b": ["bfsdifdpa", "杨振宇", "杨过"],
            "c": ["cdfdfgd", "cgfhjf", "cuyjk"],
            "d":["dfdgd","dyjhfh","dhyjgh"]
        };
        if (keyWords[this.value]) {
            //判断body中是否有这个层,如果有就删掉了
            if (document.getElementById('dv')) {
                document.body.removeChild(document.getElementById('dv'));
            }
            //开始创建层
            var dvObj = document.createElement('div');
            dvObj.id = 'dv';
            dvObj.style.width = '300px';
            //dvObj.style.height = '200px'; //将来可以不要
            dvObj.style.border = '1px solid red';
            document.body.appendChild(dvObj);
            //脱离文档流
            dvObj.style.position = 'absolute';
            dvObj.style.left = this.offsetLeft + 'px';
            dvObj.style.top = this.offsetHeight + this.offsetTop + 'px';
            //循环创建
            for (var i = 0; i < keyWords[this.value].length; i++) {
                //创建一个可以存文本的标签
                var pObj = document.createElement('p');
                pObj.innerText = keyWords[this.value][i];
                //p标签要有小手，还有高亮显示
                pObj.style.cursor = 'pointer';
                pObj.style.margin = '5px';
                pObj.onmouseover = function () {
                    this.style.backgroundColor = 'red';
                };
                pObj.onmouseout = function () {
                    this.style.backgroundColor = '';
                }
                dvObj.appendChild(pObj); //操作节点，把p标签加到层中
                //同样可以用insertBefore()来添加
            }
            //创建可以显示文件的标签
        }
    }
    //firefox下检测状态改变只能用oninput,且需要用addEventListener来注册事件。 
    if (/msie/i.test(navigator.userAgent)) //ie浏览器 
    {
        document.getElementById('txt').onpropertychange = handle
    }
    else {//非ie浏览器，比如Firefox 
        document.getElementById('txt').addEventListener("input", handle, false);
        //绑定事件对象.addEventListener(事件类型，回调函数，bool值)
        //如果不传入bool值，或者为false；事件就会走冒泡阶段；反之，事件会走捕获阶段。
    }
};
</script>
</head>
<body>
<span id="msg"></span>
请输入搜索关键字
<input type="text" name="name" value="" style="width:300px;height:30px;font-size:25px; border:1px solid green" id="txt"/>百度一下
</body>
</html>

利用JSONP调用百度接口

JSONP(JSONwith Padding)是一个非官方的协议，它允许在服务器端集成Script tags返回至客户端，通过javascript callback的形式实现跨域访问（这仅仅是JSONP简单的实现形式）。 该代码实现搬运自CSDN

实现原理：向输入框动态输入时关键词，将当前关键词作为问号参数后面的值，因为要跨域使用百度的接口，所以通过 JSONP 跨域创建 Ajax 请求。回调函数处理返回值。

1.使用 flex 布局实现搜索框的水平垂直居中。

2.先获取常用的 DOM 节点，避免后续频繁查询操作 DOM。

3.为了避免在输入过程中频繁发送请求(如果打字速度快),对请求函数做了函数节流，调了一下间隔 130ms 差不多正好，时间再长就会有卡顿的感觉。使用了 ES6 中的箭头函数避免了setTimeout 中 this 指向的问题。

4.在回调函数中：

  • 每一次执行时首先要清除建议框里的内容，不然上一次的结果还会存在建议框里！截取了结果中的前五个(如果把所有结果都展示出来感觉有点丑…百度官方是展示前四个搜索建议)
  • 结果处理完毕后，执行自执行匿名函数，删除创建的 script 标签;

5.由于 li 是动态创建的，点击 li 标签或者点击”搜索一下”跳转百度进行搜索时，利用事件冒泡原理，进行事件委托。这里没有考虑兼容性问题：

6.除了点击事件，键盘事件–回车键以及上下键都是进行事件委托进行注册的。最终能够实现键盘上下键鼠标选择，点击“搜索一下”或回车键实现跳转搜索。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
<!DOCTYPE html>
<html lang="en">

<head>
  <meta charset="UTF-8">
  <meta name="viewport" content="width=device-width, initial-scale=1.0">
  <!-- 兼容性视图 -->
  <meta http-equiv="X-UA-Compatible" content="ie=edge">
  <meta content="更方便快捷搜索，从而达到事半功倍的效果" name="description">
  <title>search you want</title>
  <style>
    html {
      height: 100%;
    }
    body {
      background: #f0f3ef;
      height: 100%;
    }
    .container {
      height: 100%;
      display: flex;
      justify-content: center;
      align-items: center;
      flex-direction: column;
    }
    .bgDiv {
      box-sizing: border-box;
      width: 595px;
      height: 55px;
      position: relative;
    /* position: absolute;
    left: 50%;
    top: 50%;
    transform: translate(-50%, -50%); */
    }
    .search-input-text {
      border: 1px solid #b6b6b6;
      width: 495px;
      background: #fff;
      height: 33px;
      line-height: 33px;
      font-size: 18px;
      padding: 3px 0 0 7px;
    }
    .search-input-button {
      width: 90px;
      height: 38px;
      color: #fff;
      font-size: 16px;
      letter-spacing: 3px;
      background: #3385ff;
      border: .5px solid #2d78f4;
      margin-left: -5px;
      vertical-align: top;
      opacity: .9;
    }
    .search-input-button:hover {
      opacity: 1;
      box-shadow: 0 1px 1px #333;
      cursor: pointer;
    }
    .suggest {
      width: 502px;
      position: absolute;
      top: 38px;
      border: 1px solid #999;
      background: #fff;
      display: none;
    }
    .suggest ul {
      list-style: none;
      margin: 0;
      padding: 0;
    }
    .suggest ul li {
      padding: 3px;
      font-size: 17px;
      line-height: 25px;
      cursor: pointer;
    }
    .suggest ul li:hover {
      background-color: #e5e5e5
    }
  </style>
</head>

<body>
  <div class="container">
    <div class="bgDiv">
      <input type="text" class="search-input-text" value="" autofocus placeholder="关键词">
      <input type="button" value="搜索一下" class="search-input-button" id="btn">
      <div class="suggest">
        <ul id="search-result">
        </ul>
      </div>
    </div>
  </div>
  <script>
    var suggestContainer = document.getElementsByClassName("suggest")[0];
    var searchInput = document.getElementsByClassName("search-input-text")[0];
    var bgDiv = document.getElementsByClassName("bgDiv")[0];
    var searchResult = document.getElementById("search-result");

    // 清除建议框内容
    function clearContent() {
      var size = searchResult.childNodes.length;
        //childNodes方法返回数组，根据数组长度判断建议框的长度
      for (var i = size - 1; i >= 0; i--) {
        searchResult.removeChild(searchResult.childNodes[i]);
      }
    };
    // 回调函数处理返回值
    function handleSuggestion(res) {
      // 清空之前的数据！！
      clearContent();
      var result = res.s;
      // 截取前五个搜索建议项
      if (result.length > 4) {
        result = result.slice(0, 5)
      }
      for (let i = 0; i < result.length; i++) {
        // 动态创建li标签
        var liObj = document.createElement("li");
        liObj.innerHTML = result[i];
        searchResult.appendChild(liObj);
      }
      // 自执行匿名函数--删除用于跨域的script标签
      (function () {
        var s = document.querySelectorAll('script');
        for (var i = 1, len = s.length; i < len; i++) {
          document.body.removeChild(s[i]);
        }
      })()
    };

    function jumpPage() {
      window.open(`https://www.baidu.com/s?word=${encodeURI(searchInput.value)}`);
    }  
     
    var timer = null;
    // 注册输入框键盘抬起事件
    searchInput.onkeyup = function (e) {
      suggestContainer.style.display = "block";
      // 如果输入框内容为空 清除内容且无需跨域请求
      if (this.value.length === 0) {
        clearContent();
        return;
      }
      if (this.timer) {
        clearTimeout(this.timer);
      }
      if (e.keyCode !== 40 && e.keyCode !== 38) {
        // 函数节流优化
        this.timer = setTimeout(() => {
          // 创建script标签JSONP跨域
          var script = document.createElement("script");
          script.src = "https://www.baidu.com/su?&wd=" + encodeURI(this.value.trim()) +
            "&p=3&cb=handleSuggestion";
          document.body.appendChild(script);
        }, 130)
      }
    };
    // 事件委托 点击li标签或者点击搜索按钮跳转到百度搜索页面
    bgDiv.addEventListener("click", function (e) {
      if (e.target.nodeName.toLowerCase() === 'li') {
        var keywords = e.target.innerText;
        searchInput.value = keywords;
        jumpPage();
      } else if (e.target.id === 'btn') {
        jumpPage();
      }
    }, false);

    var i = 0;
    var flag = 1;

    // 事件委托 监听键盘事件
    bgDiv.addEventListener("keydown", function (e) {
      var size = searchResult.childNodes.length;
      if (e.keyCode === 13) {
        jumpPage();
      };
      // 键盘向下事件
      if (e.keyCode === 40) {
        if (flag === 0) {
          i = i + 2;
        }
        flag = 1;
        e.preventDefault();
        if (i >= size) {
          i = 0;
        }
        if (i < size) {
          searchInput.value = searchResult.childNodes[i++].innerText;
        }
      };
      // 键盘向上事件
      if (e.keyCode === 38) {
        if (flag === 1) {
          i = i - 2;
        }
        flag = 0;
        e.preventDefault();
        if (i < 0) {
          i = size - 1;
        }
        if (i > -1) {
          searchInput.value = searchResult.childNodes[i--].innerText;
        }
      };
    }, false);

    // 点击页面任何其他地方 搜索结果框消失
    document.onclick = () => clearContent()
  </script>
</body>
</html>

发表于 更新于 分类于

前言

直接操作DOM已经很少在业务场景中用到了，但DOM始终作为前端的基础之一，在面试中往往总能够遇到。本文希望能够汇总以下简单的DOM知识点，让自己在沉迷框架构建时，不至于忽略或者忘记最基础的知识。主要分为两部分：1、常用的DOM方法的汇总；2、DOM的事件机制，主要是事件冒泡与事件捕获。

DOM方法

选取元素

名称选择

名称选择比较简单，主要是根据ID、name属性、标签名称、类名；来选择对应的DOM节点。

1
2
3
4
5
6
7
8
//ID选择器：基于id=""
let id =  document.getElementById("id");
//名称选择器:基于name属性
let name = document.getElementsByName("name");
//标签选择器：利用HTML元素的标签名称选取指定类型的元素
var h1 = document.getElementsByTagName("h1");
//类选择器：利用HTML的class属性值选择元素
let title = document.getElementsByClassName(title);

CSS选择

通过CSS样式表选择器的强大语法，也可以来选择元素，返回第一个匹配的元素，或者返回元素数组。

1
2
3
var title = document.querySelector("#title");   // CSS ID选择
var h1 = document.querySelector("h1");     //选取第一个h1元素
var h1s = document.querySelectorAll("h1");   //返回所有h1标签元素

相近节点选取

节点：页面中所有的内容都是节点（标签，属性，文本：文字，空格，换行）文档：document—-页面中的顶级对象元素：页面中所有的标签，标签–元素–对象（通过DOM的方式来获取这个标签，得到了这个对象，此时这个对象叫DOM对象）。

关于节点的选取有如下的方法：

1
2
3
4
5
6
7
8
9
h1.parentNode;//父节点
h1.childNodes;//以数组形式返回子节点
h1.firstChild; h1.lastChild;
h1.nextSibling;//下一个兄弟节点
h1.previousSibling;//前一个兄弟节点
h1.nodeType;
//返回节点类型的数字表示：1-element节点；3-text节点；8-comment节点；9-document节点；11-documentFragment节点
h1.nodeValue;//返回Text 节点 或 Comment 节点的值
h1.nodeName;//返回元素的标签名，以大写形式表示

元素相关的选取同样有如下的方法：

1
2
3
4
h2.children;//以数组的形式返回所有的子元素
h2.firstElementChild; h2.lastElementChild;//返回首子元素与尾子元素
h2.nextElementSibling; h2.previousElementSibling;//返回上一兄弟元素与下一兄弟元素
h2.childElementCount;//返回子元素数量

属性相关

表示HTML文档元素的HTMLElement对象定义了读/写属性，它们对应于元素的HTML属性。 HTMLElement定义的通用HTML属性，包括id、lang、dir、事件处理程序onclick及表单相关属性等。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
h3.getAttribute("width");//返回非标准的HTML属性的值
h3.setAttribute("width", "150px");//设置非标准的HTML属性的值
h3.hasAttribute("height");//判断属性是否存在
h3.removeAttribute("width");//删除某一属性
//在HTML5文档中，任意以 data- 为前缀的小写的属性名字都是合法的。这些 “数据集属性” 定义了一种标准的、附加额外数据的方法
//以data-x = ""为例
h3.dataset.x;
//Node节点定义了 attributes 属性，针对 Element 对象，attributes 是元素所有属性的类数组对象
//索引 attributes 对象得到的值是 Attr 对象。Attr 的 name 和 value 返回该属性的名字和值
let a = h3.attributes.src.value;

h4.innerHTML;//以字符串形式返回这个元素的内容。 也可以用来替换元素当前内容
h4.outerHTML;//以字符串形式返回这个元素及内容。 也可以用来替换元素当前内容
h4.textContent;//查询或替换纯文本元素内容的标准方法是用Node的textContent属性来实现。

创建节点

1
2
3
4
5
6
document.createElement("h1");//使用document 对象的createElement () 方法创建新的Element节点
document.createTextNode("文本节点");//创建纯文本节点
document.createDocumentFragment();//创建文档片段，往往有更好性能
//因为文档片段存在于内存中，并不在Dom树中，所以将子元素插入到文档片段时不会引起页面回流 （对元素位置和几何上计算）
document.createCmoment("....");//创建注释节点
h4.cloneNode(true);//通过复制已存在的节点来创建新的文档节点。传参数true表示深克隆，false表示浅复制

插入、修改节点

1
2
3
4
5
6
7
8
h5.appendChild("h1");//在指定元素上插入子节点，并使其成为该节点的最后一个子节点
//一般先新建子节点，再插入子节点
h5.insertBefore("h1", "h2");
//1. 在父节点上调用本方法2. 第一参数表示待插入的节点
//3. 第二参数是父节点中已经存在的子节点，新节点插入到该节点的前面
h5.removeChild("h2");//在父节点中调用，参数是待删除的节点
h5.replaceChild("h2,", "h2");
//1. 在父节点上调用;2. 第一参数是新节点;3. 第二个参数是需要替换的节点

DOM事件机制

1、事件是在编程时系统内发生的动作或者发生的事情

2、事件是要绑定在元素上的。比如给一个div元素绑定一个鼠标悬浮事件，给一个ol元素绑定鼠标单击事件。

3、可以使用事件监听函数（也叫事件处理程序、侦听器）来监听事件，以便事件发生时执行相应的代码

事件发生时元素节点之间按照特定的顺序传播，这个过程即DOM事件流，描述的是从页面接收事件的顺序。

冒泡与捕获

首先开始事件捕获阶段：从DOM树最根部的节点window开始，沿着DOM树向下遍历每个元素，直到触发元素目标元素target。如果这些元素也注册了click事件（且为捕获阶段），就会执行他们相应的事件监听函数。即从上到下触发父元素对应的事件。在事件捕获这一阶段，为截获事件提供了机会。

当前目标阶段：实际的目标接收到，并执行对应得事件监听函数。

事件冒泡阶段：从触发元素目标元素target开始，向上逆着遍历DOM树，直到最根部window元素。如果这些元素也注册了click事件（且为冒泡阶段），就会执行他们相应的事件监听函数

我们在使用 addEventListener 监听事件时，addEventListener(‘click’, fn, bool)如果第三个参数 bool 不传，或者传 false, 那么我们会在冒泡阶段调用 fn如果第三个参数 Bool 传值为 true, 那么我们会在捕获阶段调用 fn。因此，默认是在冒泡阶段来监听事件的。

捕获不可以取消，但是冒泡可以取消，e.propagation()就可但是有一些事件不可以取消冒泡，比如 scroll 事件。

1
2
3
4
5
6
<div>
  <span>文字</span>
</div>
e.target 用户正在操作的元素
e.currentTarget 程序员在监听的元素
假设我们监听的是 div, 但用户实际点击的是文字，那么e.target 就是 span 标签,e.currentTarget 就是 div 标签。

事件委托

冒泡阶段，浏览器从用户点击的内容从下往上遍历至 window，逐个触发事件处理函数，因此可以监听一个祖先节点(例如爸爸节点、爷爷节点)来同时处理多个子节点的事件。

主要的作用有：1、省掉监听数，节省内存；要监听多个兄弟元素时，不如只监听父元素，并在事件处理函数中，利用e.target来判断到底是哪一个子元素触发了事件，再进行对应的处理即可。

2、监听不存在的元素，即动态元素。

发表于 更新于 分类于

源码思维

健壮性

代码在发生预期之外的错误时，其应对错误的能力：即就算出错也能够轻松定位到错误，且减少错误的影响范围。

1
2
3
4
5
6
7
8
9
10
11
//1、不要轻易去相信传入参数，需要判断参数类型
function add(a, b) {
    if (typeof a == 'number' && typeof b == 'number') {
        return a + b;
    } else {
        throw new Error('a');
    }
}

//2、易错代码用try catch包裹起来
a[0] && a[0].data[0];//取属性之前，先判断其是否存在

defineProperty

主要用于vue的数据绑定，

使用defineProperty中的get来进行设置属性时，这个属性不能被改值，因为只写了get，只能够取到值而不能改值；要能够改值则需要写上set。其实这是一种变量权限的问题，如果该变量是某个属性的话，则可以使用defineProperty来控制其各类权限。

1
2
3
4
5
6
this.$router = this._root._router;
Object.defineProperty(this, '$router', {
    get() {
        return this._root._router;
    }
});

模块支持检测：先判断当前的环境符合的哪种模块规范；cmd、amd、umd，或者CommonJS规范、import规范。

架构模式

工厂模式

通俗而讲：我去构建一个工厂方法，让使用者调用这个工厂方法去拿到他要的对象，而不是自己去构建，即不需要去new。

典型例子：jquery。使用jquery时是DOM时代，频繁获取并操作DOM。工厂模式直接用$()就可以拿到对象。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//jQuery
(function(window) {
    function jquery() {
        return new jquery.fn.init();
    }
    jquery.fn.init.prototype = jquery.fn;
    jquery.fn = jquery.prototype = {
        init:function() {
            
        }
    }
    jquery.extend({
        //回调。给一个对象，将其添加到jquery上
    })
    //这样去包装是为了jquery中的方法可以有多种调用方式，
    //但对象为引用类型，var b = {}, a = b, c = b,修改b时a、c均会修改，实现改一个均影响到。
    window.$ = window.jquery = jquery;
})(window);//定义一个匿名自执行函数，不污染外部全局变量，
//同时后面直接传参(window),减少作用链长度

//vue
(function (global, factory) {
    
}(this, function () {
    
}));//this在浏览器环境为window，在node环境为global，不会去写死

建造者模式

在构建一个庞大的框架时，先把整个框架分开成几个模块，=》预制=》然后将各个模块融合在一起。

典型例子：vue-2，构建一个庞大的框架。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
function Vue(options) {
    if (!(this instanceof Vue)) {
        warn('Vue is a constructor');
    }
    this._init(options);
}

initMixin(Vue);
stateMixin(Vue);
eventsMixin(Vue);
lifecycleMixin(Vue);
renderMixin(Vue);
/*为什么非要分开开发，而不是全部放到原型链上即可。
1、由于是团队开发，全放在prototype，可能会收到相互之间的影响

*/

函数式

整体的功能就是一大堆的函数，通过函数之间的相互调用来实现整体的功能。对于javaScript，函数才是一等公民：1、tree-shaking：基于文档流的原理，判断某个函数是否被调用，因此能够webpack时自动删除未被调用的函数。2、组合大于继承。因此函数式编程适用于工具库。

典型例子：Vue3，

设计模式

vue-router、vuex这样的只能有一个，即典型的一个类只有一个实例化对象，即单例模式。实现很容易，就是先判断是否已经被实例化过，如果已经实例化过，就不再实例化；需要通过一个变量判断是否已经实例化过。

1
2
3
4
5
6
7
var _vue;
function install(vue) {
    if (install.installed && _vue == vue) return;
    //执行安装
    install.installed = true;
    _vue = vue;
}

代码简洁技巧：jquery中的extend({})方法，传入两个对象时，会将两个对象合并再传入。享元模式：减少重复的代码块的数量，将不同点提取出来作为参数。

1
2
3
4
5
6
7
8
9
10
11
function () {
    let target = this;
    let source = arguments[0];
    if (arguments.length == 2) {
        target = this;
        source = arguments[1];
    }
    for (let item in source) {
        target[item] = source[item];
    }
}

优雅利用原生方法：vue使用defineProperty来实现双向绑定，但只能应用于对象的属性；那么数组怎么来触发更新？将数组原生的push、pop、shift方法加上了能够触发双向绑定的功能。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
let arr = ["push", "pop"];
var arrayProto = Array.prototype;
let arrayMethods = Object.create(arraryProto);
//执行以下拷贝，来避免污染原生的原型链
arr.forEach((methos) => {
    arrMethods[method] = function() {
        let original = arrayProto[method];
        let result = original.apply(this, args);
        //先找到需要修改的方法，并先将原生方法的功能附加上去；
        dep.noyify();//触发数组更新
        return result;//保持返回值与原方法一致
        //最后只替换数组中的原型链即可
    }
})

应用进阶

缓存架构-API

优化方案：快、小、省。

缓存：是所有优化方案里最常用、最有效、可以节省http请求，可以从内存中最快读取数据。

1、选择更快的API、算法，减少时间复杂度；

2、看到网站主要消耗的时间，更多地并不在于代码的执行速度，而在于资源加载的速度，因此文件体积小更重要。一、用webpack压缩treeshaking；二、减少代码重复；

vue3方面的改进：1、快：更快的API，用proxy来代替defineProperty；代理proxy不会去改变原对象；diff算法方面改进：对比新老的DOM，先分析动态DOM，只比对动态的DOM；2、小：函数式API：拥抱tree-shaking，可以很方便地将没有用到的方法取出来，并不附加在工程文件中。

3、省：节省http请求

读取数据的快慢：最慢：网络请求；其次：从硬盘中拿数据；最快：从内存中拿数据。因此请求缓存思路就是：有缓存的话，不去发送请求而是直接从缓存中拿去数据。

缓存架构的技巧：

1、缓存架构需要使用单例模式，即所有的缓存都放在一个里面。

2、权限问题，存缓的区域不能直接拿出去给别人操作。因此，需要隐藏起来，使用匿名自执行函数来进行；但同样，需要外界能够进行读取缓存操作，因此需要返回一个对象，在该对象内有一系列操作缓存的方法。这其实是函数闭包的应用。

3、缓存都会存在副作用：

一、更新问题：使用localstorage、session、cookies缓存时，缓存至本地，需要考虑更新问题。(1)、与后端进行websocket连接，但过于麻烦，没必要；(2)、通过定期轮询，定时器，每隔一段时间向后端发起ajax请求；经常变动的API不要用这种缓存；

使用内存缓存时，是不用考虑更新问题；但内存缓存同样有自己的问题，需要考虑占用内存问题，每往里面加东西，都会占用内存。javascript的内存限制较严重，因此需要做一个限制。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
if (!window.mycache) {
    window.mycache = (function() {
        var cache = {};
        var cacheArr = [];
        return {
            get: function (api) {
                return new Promise(() => {
                    //promise实现异步以及链式调用
                 if (cache[api]){
                    resolve(cache[api])
                } else {
                    this.set(api).then(()=> {
                        if (cacheArr.length > 10) {
                            let _api = cacheArr.shift();
                            this.remove(_api);
                        }
                        cache[api] = res;
                        cacheArr.push(api);
                        //需要确保内存限制，不要占用太多内存
                        resolve(res);
                    })
                }
                })
            },
            set: function () {
                return axios.get(api);
            },
            remove: function () {
                
            }
        }
    })();
    //放在匿名自执行函数里面
}

vue插件

关键的两个API：Vue.use；Vue.mixin。

Vue.use();原理：将一个方法执行一次，如果该方法中有install属性，就执行其install属性，来代替执行该方法；

Vue.mixin()；原理：相当于一个全局混合；(局部混合相当于在组件的export后写mixin)，可以混合方法methods、数据data、混合生命周期(生命周期的混入才是核心功能)。即，混入的生命周期操作，所有的组件在对应的生命周期均执行该操作函数。

打包项目=》打包体积过大，可以使用异步加载来减少体积 =》 vuex内容太大；=》vuex异步加载，根据组件来异步加载vuex，放在beforeCreated阶段，在DOM还没有加载好之前，将其之间的依赖关系读取好。

插件的用途：1、提供逻辑复用；2、注入自定义操作；

常用API

Vue.util.defineReative：其实就是Vue自身去做响应式的方法，；一般来说只有data的数据能触发响应。这里，我们可以调用这个API，使外部数据也能触发响应。

用法：1、将localstorage中的数据触发响应，不需要将其取出来；2、监听window的事件，常用的是resize，实现尺寸的自适应；3、监听浏览器版本、内存；

本质是让外部数据也能触发响应。

Vue.extend：传入一个对象时，其会返回一个构造函数，直接new便可以创建实例。用于import，在使用import时，导入的是vue的选项。

vue单元测试=》测某个组件的方法和节点渲染结果

render渲染：提供函数，用JS来表达你的整个template，当页面的逻辑较为复杂时。

API层

Axios源码分析

Axios如何实现请求拦截、响应拦截

1、初始化Axios，其实是调用request方法；

请求拦截器设置的处理——发送请求——响应拦截器设置的处理：这些一大堆方法由数组来存储；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
axios.interceptors.request.use(()=> {
    
})
axios.interceptors.response.use(()=> {
    
})
function axios() {
    this.interceptors = {
        request: new interceptorsManner(),
        response: new interceptorsManner()
    }
}
function interceptorsManner(){
    this.handlers = [];
}
interceptorsManner.prototype.use((fullfilled, rejected) => {
    this.handler.push({
        fullfilled: fullfilled;
        rejected: rejectes;
    })
})

发表于 更新于 分类于

表单组件

简单地自己造一下轮子，实现一下vue的自定组件，这里主要先从form组件开始实践。

form组件需求分析：1、指定数据、校验规则；高内聚、低耦合；

2、这里为了实现form组件的输入功能，我们自定义一个input组件来实现；为保证低耦合性，仅使用并实现双向绑定基本功能。

3、校验的实现跟input分开，再自定义一个KFormItem组件来实现校验的功能。执行校验的组件为KFormItem组件，但通知父组件执行校验的是其子组件KINput，由于事件是谁派发谁监听，不能用this.$emit，需要用this.parent.$emit。之后，在KFormItrm组件上监听校验事件，执行具体校验。

Input

实现功能：维护数据；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
<template>
  <div>
    <!-- 自定义组件双向绑定：:value  @input -->
    <!-- v-bind="$attrs"展开$attrs 
$attrs/$listeners包含了父作用域中不作为 prop 被识别 (且获取) 的特性绑定 ( class 和 style 除外)。当一个组件没有
声明任何 prop 时，这里会包含所有父作用域的绑定 ( class 和 style 除外)，并且可以通过 v-bind="$attrs" 传入内部组件——在创建高级别的组件时非常有用。-->
    <input :type="type" :value="value" @input="onInput" v-bind="$attrs">
  </div>
</template>

<script>
  export default {
    inheritAttrs: false, // 设置为false避免设置到根元素上，
    props: {
      value: {
        type: String,
        default: ''
      },
      type: {
        type: String,
        default: 'text'
      }
    },
    methods: {
      onInput(e) {
        // 派发一个input事件即可，相当于在原生input上面再封装一个实现了双向绑定的input
        this.$emit('input', e.target.value)

        // 通知父级执行校验
        this.$parent.$emit('validate')
      }
    },
  }
</script>

<style scoped>

</style>

KFormItem

KformItem组件包裹Input组件，同时在前面添加label标签；

实现功能：1、执行校验2、显示错误信息

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
<template>
  <div>
    <!-- label -->
    <label v-if="label">{{label}}</label>
    <slot></slot>

    <!-- 校验信息显示 -->
    <p v-if="error">{{error}}</p>
  </div>
</template>

<script>
// Asyc-validator
import Schema from "async-validator";

export default {
  inject: ["form"],
  data() {
    return {
      error: "" // error是空说明校验通过
    };
  },
  props: {
    label: {
      type: String,
      default: ""
    },
    prop: {
      type: String
    }
  },
  mounted() {
    this.$on("validate", () => {
      this.validate();
    });
  },
  methods: {
    validate() {
      // 规则
      const rules = this.form.rules[this.prop];
      // 当前值
      const value = this.form.model[this.prop];

      // 校验描述对象
      const desc = { [this.prop]: rules };
      // 创建Schema实例
      const schema = new Schema(desc);
      return schema.validate({ [this.prop]: value }, errors => {
        if (errors) {
          this.error = errors[0].message;
        } else {
          // 校验通过
          this.error = "";
        }
      });
    }
  }
};
</script>

<style scoped>
</style>

KForm

一层层地往上面的层级进行靠近，在KForm的层级，除了实现slot将下面的层级包裹，同样也要接受数据并处理。

最终目的是在KForm上除了接受数据模型model以外，还要声明校验规则rules，因此声明数据model、rules。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
<template>
  <div>
    <slot></slot>
  </div>
</template>

<script>
export default {
  provide() {
    return {
      form: this
    };//直接将组件自己传递出去，这样就能够在下面子组件拿到model、rules
  },
  props: {
    model: {
      type: Object,
      required: true
    },
    rules: {
      type: Object
    }
  },
  methods: {
    validate(cb) {
      // 获取所有孩子KFormItem
      // [resultPromise]
      const tasks = this.$children
        .filter(item => item.prop) // 过滤掉没有prop属性的Item
        .map(item => item.validate());

      // 统一处理所有Promise结果
      Promise.all(tasks)
        .then(() => cb(true))
        .catch(() => cb(false));
    }
  }
};
</script>

<style scoped>
</style>

Index

这样，在index层级里面，我们将所有的自定义组件封装起来，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
<template>
  <div>
    <!-- <ElementTest></ElementTest> -->

    <!-- KForm -->
    <KForm :model="userInfo" :rules="rules" ref="loginForm">
      <!-- 用户名 -->
      <KFormItem label="用户名" prop="username">
        <KInput v-model="userInfo.username" placeholder="请输入用户名"></KInput>
      </KFormItem>
      <!-- 密码 -->
      <KFormItem label="密码" prop="password">
        <KInput type="password" v-model="userInfo.password" placeholder="请输入密码"></KInput>
      </KFormItem>
      <!-- 提交按钮 -->
      <KFormItem>
        <button @click="login">登录</button>
      </KFormItem>
    </KForm>
  </div>
</template>

<script>
import ElementTest from "@/components/form/ElementTest.vue";
import KInput from "@/components/form/KInput.vue";
import KFormItem from "@/components/form/KFormItem.vue";
import KForm from "@/components/form/KForm.vue";
import Notice from "@/components/Notice.vue";

export default {
  data() {
    return {
      userInfo: {
        username: "tom",
        password: ""
      },
      rules: {
        username: [{ required: true, message: "请输入用户名称" }],
        password: [{ required: true, message: "请输入密码" }]
      }
    };
  },
  components: {
    ElementTest,
    KInput,
    KFormItem,
    KForm
  },
  methods: {
    login() {
      this.$refs["loginForm"].validate(valid => {
        const notice = this.$create(Notice, {
          title: "",
          message: valid ? "请求登录!" : "校验失败!",
          duration: 2000
        });
        notice.show();
        // if (valid) {
        //   alert("submit");
        // } else {
        //   console.log("error submit!");
        //   return false;
        // }
      });
    }
  }
};
</script>

<style scoped>
</style>

VueRouter

需求分析

1、作为一个插件存在：实现VueRouter类和install方法

2、实现两个全局组件：router-view用于显示匹配组件内容，router-link用于跳转

3、监控url变化：监听hashchange或popstate事件

4、响应最新url：创建一个响应式的属性current，当它改变时获取对应组件并显示

实现VueRouter插件

在toyRouter.js里面，我们需要实现一个插件，先创建VueRouter类，并且实现其install方法，该方法会在当前的Vue原型链上挂载$router。使用vue.mixin来混入生命周期中，保证每个vue均能实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class KVueRouter {
  constructor(options) {
    this.$options = options
    console.log(this.$options);
    

KVueRouter.install = function (_Vue) {
  // 保存构造函数，在KVueRouter里面使用
  Vue = _Vue;

  // 挂载$router
  // 怎么获取根实例中的router选项,混入生命周期钩子即可，该生命周期钩子会在所有组件都执行一遍
  //为什么要用混入方式写？主要原因是Vue.use(VueRouter)代码在前，Router实例创建在后，而install逻辑又需要用到该实例
  Vue.mixin({
    beforeCreate() {
      // 确保根实例的时候才执行，只有根实例有router选项
      if (this.$options.router) {
        Vue.prototype.$router = this.$options.router
      }
    }
  })
}

export default KVueRouter

为实现功能，将其写成独立的组件，并在vueRouter的install方法中再将其引入。

router-link实现的功能是：解析用户输入的路由值，并重新渲染一个输入路由值对应的a标签。且在纯运行时的环境，不能使用template而需要用render函数来渲染页面，这里我们需要渲染一个a标签。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
export default {
  props: {
    to: {
      type: String,
      required: true
    },
  },
  render(h) {
    // <a href="#/about">abc</a>
    // <router-link to="/about">xxx</router-link>，值是用户通过props传进来的，因此直接用this.to，前面拼上#为了使用方便
    // h(tag, data, children)
    console.log(this.$slots);
    return h('a', { attrs: { href: '#' + this.to } }, this.$slots.default)
    // return <a href={'#' + this.to}>{this.$slots.default}</a>
  }
}

router-view

router-view实现的功能基本上是：根据当前的路由值，获取对应的component并渲染在当前位置。

1、需要监控路由的变化，且为了实现路由改变时，便实时刷新页面，因此需要设置当前路由值为响应式数据。

2、为了确保查找的快速，在新建VueRouter时就应该以用户输入路由配置，初始化一个hash表，这样每次获取当前路由值的component时，只用O(1)时间即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
//上述两点应该在VueRouter类中实现，因此VueRouter更新为：
class KVueRouter {
  constructor(options) {
    this.$options = options
    console.log(this.$options);
    // 需要创建响应式的current属性，当当前路由路径发生变化时，则页面就会重新渲染，这就是响应式
    // 利用Vue提供的defineReactive做响应化
    // 这样将来current变化的时候，依赖的组件会重新render
    Vue.util.defineReactive(this, 'current', '/')

    // this.app = new Vue({
    //   data() {
    //     return {
    //       current: '/'
    //     }
    //   }
    // })
    
    // 监控url变化，利用bind锁定this，避免你使用的onHashChange函数的this变成后面的window
    window.addEventListener('hashchange', this.onHashChange.bind(this))
    window.addEventListener('load', this.onHashChange.bind(this))//除了路由修改以外，用户刷新页面也要有重新渲染


    // 创建一个路由映射表
    this.routeMap = {}
    options.routes.forEach(route => {
      this.routeMap[route.path] = route
    })
  }

  onHashChange() {
    console.log(window.location.hash);
    this.current = window.location.hash.slice(1);//由于前面还有#号，因此需要slice切割一下
  }
}

而在router-view页面要实现的功能就要简单些了，主要是从路由映射hsahMap中获取对应组件，这里同样要用render函数来渲染。

1
2
3
4
5
6
7
8
9
10
export default {
  render(h) {
    //获取path对应的component
    const {routeMap, current} = this.$router;//从路由映射中找到对应的路由，用hash表来查找，快速找到结果
    console.log(routeMap,current);
    
    const component = routeMap[current].component || null;
    return h(component)
  }
}

Vuex

目的：集中管理数据、可预测的改变数据；类似于整个项目数据的大管家，确保整个程序的状态、数据能够保持同步的状态，维持稳定。

需求分析

1、实现一个插件：声明Store类，挂载$store

2、：创建响应式的state，保存mutations、actions和getters

3、实现commit根据用户传入type执行对应mutation

4、实现dispatch根据用户传入type执行对应action，同时传递上下文

5、实现getters，按照getters定义对state做派生

实现store插件

声明Store、install方法，并创建一个响应式的state。同时利用存取器，避免用户直接去取state

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
// 保存构造函数引用，避免import
let Vue;

class Store {
  constructor(options) {
    // this.$options = options;
    this._mutations = options.mutations;
    this._actions = options.actions;

    // 响应化处理state
    // this.state = new Vue({
    //   data: options.state
    // })
    this._vm = new Vue({
      data: {
        // 加两个$，Vue不做代理，因此对外部是隐藏的，不能直接去访问。
        $$state: options.state
      }
    })

    // 绑定commit、dispatch的上下文问store实例
    this.commit = this.commit.bind(this)
    this.dispatch = this.dispatch.bind(this)
  }

  // 存取器， 用户通过store.state的方式来访问，这样避免用户直接修改state。
    //官方的实现是：使用一个watch去监听任何修改，一旦用户尝试修改，则直接报错。
  get state() {
    console.log(this._vm);
    return this._vm._data.$$state
  }

  set state(v) {
    console.error('无法修改！');
    
  }

function install(_Vue) {
  Vue = _Vue;

  Vue.mixin({
    beforeCreate() {
      if (this.$options.store) {
        Vue.prototype.$store = this.$options.store
      }
    }
  })
}

// Vuex
export default {
  Store,
  install
}

实现commit、dispatch方法

在写方法之前需要将this.commit、this.dispatch绑定为该store实例，在构造函数上加上：this.commit = this.commit.bind(this)；this.dispatch = this.dispatch.bind(this)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Store {
    /*
    在写方法之前需要将this.commit、this.dispatch绑定为该store实例，在构造函数上加上：
    this.commit = this.commit.bind(this);
    this.dispatch = this.dispatch.bind(this);
    */
   
  // store.commit('add', 1)
  // type: mutation的类型
  // payload：载荷，是参数
  commit(type, payload) {
    const entry = this._mutations[type]
    if (entry) {
      entry(this.state, payload)
    }
  }

  dispatch(type, payload) {
    const entry = this._actions[type]
    if (entry) {
      entry(this, payload)
    }
  }
}

实现getters

发表于 更新于 分类于

二叉搜索树的操作集锦

总路线

⼆叉树算法的设计的总路线：明确⼀个节点要做的事情，然后剩下的事抛给 框架。

1
2
3
4
5
6
void traverse(TreeNode root) { 
    // root 需要做什么？在这做。 
    // 其他的不⽤ root 操⼼，抛给框架 
    traverse(root.left); 
    traverse(root.right); 
}

如何把⼆叉树所有的节点中的值加⼀？

1
2
3
4
5
6
void plusOne(TreeNode root) { 
    if (root == null) return; 
    root.val += 1; 
    plusOne(root.left); 
    plusOne(root.right); 
}

如何判断两棵⼆叉树是否完全相同？

1
2
3
4
5
6
7
8
9
10
11
boolean isSameTree(TreeNode root1, TreeNode root2) { 
    // 都为空的话，显然相同 
    if (root1 == null && root2 == null) return true;
    // ⼀个为空，⼀个⾮空，显然不同 
    if (root1 == null || root2 == null) return false; 
    // 两个都⾮空，但 val 不⼀样也不⾏ 
    if (root1.val != root2.val) return false; 
    // root1 和 root2 该⽐的都⽐完了 
    return isSameTree(root1.left, root2.left) 
        && isSameTree(root1.right, root2.right); 
}

借助框架可以理解上述两个例子，那么就能解决所有二叉树算法。

二叉搜索树BST是一种很常用的二叉树，定义为：一个二叉树中，任意节点的值要大于等于左子树所有节点的值，且要小于等于右边子树所有节点的值。

基础操作有：判断合法性、增、删、查。

判断BST的合法性

这⾥是有坑的哦，我们按照刚才的思路，每个节点⾃⼰要做的事不就是⽐较 ⾃⼰和左右孩⼦吗？看起来应该这样写代码：

1
2
3
4
5
6
7
boolean isValidBST(TreeNode root) { 
    if (root == null) return true; 
    if (root.left != null && root.val <= root.left.val) return false; 
    if (root.right != null && root.val >= root.right.val) return false; 
    return isValidBST(root.left) 
        && isValidBST(root.right); 
}

但是这个算法出现了错误，BST 的每个节点应该要⼩于右边⼦树的所有节 点，下⾯这个⼆叉树显然不是 BST，但是我们的算法会把它判定为 BST。出现错误，不要慌张，框架没有错，⼀定是某个细节问题没注意到。我们重 新看⼀下 BST 的定义，root 需要做的不只是和左右⼦节点⽐较，⽽是要整 个左⼦树和右⼦树所有节点⽐较。怎么办，鞭⻓莫及啊！

这种情况，我们可以使⽤辅助函数，增加函数参数列表，在参数中携带额外 信息，请看正确的代码：

1
2
3
4
5
6
7
8
9
boolean isValidBST(TreeNode root) { 
    return isValidBST(root, null, null); 
}
boolean isValidBST(TreeNode root, TreeNode min, TreeNode max) { 
    if (root == null) return true; 
    if (min != null && root.val <= min.val) return false; 
    if (max != null && root.val >= max.val) return false; 
    return isValidBST(root.left, min, root) 
        && isValidBST(root.right, root, max); }

在BST中查找一个数是否存在

根据我们的指导思想，可以这样写代码： 

1
2
3
4
5
6
7
boolean isInBST(TreeNode root, int target) { 
    if (root == null) return false; 
    if (root.val == target) return true; 
    
    return isInBST(root.left, target) || 
        isInBST(root.right, target); 
}

这样写完全正确，充分证明了你的框架性思维已经养成。现在你可以考虑⼀ 点细节问题了：如何充分利⽤信息，把 BST 这个“左⼩右⼤”的特性⽤上？ 很简单，其实不需要递归地搜索两边，类似⼆分查找思想，根据 target 和 root.val 的⼤⼩⽐较，就能排除⼀边。我们把上⾯的思路稍稍改动：

1
2
3
4
5
6
7
8
9
10
boolean isInBST(TreeNode root, int target) { 
    if (root == null) return false; 
    if (root.val == target) 
        return true; 
    if (root.val < target) 
        return isInBST(root.right, target);
    if (root.val > target) 
        return isInBST(root.left, target); 
    // root 该做的事做完了，顺带把框架也完成了，妙 
}

于是，我们对原始框架进⾏改造，抽象出⼀套针对 BST 的遍历框架：

1
2
3
4
5
6
7
8
void BST(TreeNode root, int target) { 
    if (root.val == target) 
        // 找到⽬标，做点什么 
    if (root.val < target) 
            BST(root.right, target);
    if (root.val > target) 
            BST(root.left, target); 
}

在 BST 中插⼊⼀个数

对数据结构的操作⽆⾮遍历 + 访问，遍历就是“找”，访问就是“改”。具体到 这个问题，插⼊⼀个数，就是先找到插⼊位置，然后进⾏插⼊操作。

上⼀个问题，我们总结了 BST 中的遍历框架，就是“找”的问题。直接套框 架，加上“改”的操作即可。⼀旦涉及“改”，函数就要返回 TreeNode 类型， 并且对递归调⽤的返回值进⾏接收。

1
2
3
4
5
6
7
8
9
10
11
12
TreeNode insertIntoBST(TreeNode root, int val) { 
    // 找到空位置插⼊新节点 
    if (root == null) 
        return new TreeNode(val); 
    // if (root.val == val) 
    // BST 中⼀般不会插⼊已存在元素 
    if (root.val < val) 
        root.right = insertIntoBST(root.right, val); 
    if (root.val > val) 
        root.left = insertIntoBST(root.left, val); 
    return root; 
}

在 BST 中删除⼀个数

这个问题稍微复杂，不过你有框架指导，难不住你。跟插⼊操作类似， 先“找”再“改”，先把框架写出来再说： 

1
2
3
4
5
6
7
8
9
10
11
TreeNode deleteNode(TreeNode root, int key) { 
    if (root.val == key) { 
        // 找到啦，进⾏删除 
    } 
    else if (root.val > key) { 
        root.left = deleteNode(root.left, key); 
    } else if (root.val < key) { 
        root.right = deleteNode(root.right, key); 
    }
    return root; 
}

找到⽬标节点了，⽐⽅说是节点 A，如何删除这个节点，这是难点。因为删 除节点的同时不能破坏 BST 的性质。有三种情况，⽤图⽚来说明。

情况 1：A 恰好是末端节点，两个⼦节点都为空，那么它可以当场去世了。

情况 2：A 只有⼀个⾮空⼦节点，那么它要让这个孩⼦接替⾃⼰的位置。

情况 3：A 有两个⼦节点，⿇烦了，为了不破坏 BST 的性质，A 必须找到 左⼦树中最⼤的那个节点，或者右⼦树中最⼩的那个节点来接替⾃⼰。我们 以第⼆种⽅式讲解。

三种情况分析完毕，填⼊框架，简化⼀下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
TreeNode deleteNode(TreeNode root, int key) { 
    if (root == null) return null; 
    if (root.val == key) { 
        // 这两个 if 把情况 1 和 2 都正确处理了 
        if (root.left == null) return root.right; 
        if (root.right == null) return root.left; 
        // 处理情况 3 
        TreeNode minNode = getMin(root.right); 
        root.val = minNode.val; 
        root.right = deleteNode(root.right, minNode.val); 
    } else if (root.val > key) { 
        root.left = deleteNode(root.left, key); 
    } else if (root.val < key) { 
        root.right = deleteNode(root.right, key); 
    }
    return root; 
}

TreeNode getMin(TreeNode node) { 
    // BST 最左边的就是最⼩的 
    while (node.left != null) node = node.left; 
    return node; 
}

删除操作就完成了。注意⼀下，这个删除操作并不完美，因为我们⼀般不会 通过 root.val = minNode.val 修改节点内部的值来交换节点，⽽是通过⼀系列 略微复杂的链表操作交换 root 和 minNode 两个节点。因为具体应⽤中，val 域可能会很⼤，修改起来很耗时，⽽链表操作⽆⾮改⼀改指针，⽽不会去碰 内部数据。

但这⾥忽略这个细节，旨在突出 BST 基本操作的共性，以及借助框架逐层 细化问题的思维⽅式。

总结

通过这篇⽂章，你学会了如下⼏个技巧：

1、⼆叉树算法设计的总路线：把当前节点要做的事做好，其他的交给递归

框架，不⽤当前节点操⼼。

2、如果当前节点会对下⾯的⼦节点有整体影响，可以通过辅助函数增⻓参

数列表，借助参数传递信息。

3、在⼆叉树框架之上，扩展出⼀套 BST 遍历框架：

1
2
3
4
5
6
7
8
void BST(TreeNode root, int target) { 
    if (root.val == target) ;
        // 找到⽬标，做点什么 
    if (root.val < target) 
            BST(root.right, target); 
    if (root.val > target) 
        BST(root.left, target); 
}

4、掌握了 BST 的基本操作。

快速计算完全⼆叉树的节点

如果让你数⼀下⼀棵普通⼆叉树有多少个节点，这很简单，只要在⼆叉树的 遍历框架上加⼀点代码就⾏了。

但是，如果给你⼀棵完全⼆叉树，让你计算它的节点个数，你会不会？算法 的时间复杂度是多少？这个算法的时间复杂度应该是 O(logN*logN)，如果 你⼼中的算法没有达到⾼效，那么本⽂就是给你写的。

⾸先要明确⼀下两个关于⼆叉树的名词「完全⼆叉树」和「满⼆叉树」。 我们说的完全⼆叉树如下图，每⼀层都是紧凑靠左排列的： 我们说的满⼆叉树如下图，是⼀种特殊的完全⼆叉树，每层都是是满的，像 ⼀个稳定的三⾓形：

具体方法

如果是一个普通二叉树，显然只要向下面这样遍历一边即可，时间复杂度 O(N)：

1
2
3
4
public int countNodes(TreeNode root) {
    if (root == null) return 0;
    return 1 + countNodes(root.left) + countNodes(root.right);
}

那如果是一棵满二叉树，节点总数就和树的高度呈指数关系，时间复杂度 O(logN)：

1
2
3
4
5
6
7
8
9
10
public int countNodes(TreeNode root) {
    int h = 0;
    // 计算树的高度
    while (root != null) {
        root = root.left;
        h++;
    }
    // 节点总数就是 2^h - 1
    return (int)Math.pow(2, h) - 1;
}

完全二叉树比普通二叉树特殊，但又没有满二叉树那么特殊，计算它的节点总数，可以说是普通二叉树和完全二叉树的结合版，先看代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public int countNodes(TreeNode root) {
    TreeNode l = root, r = root;
    // 记录左、右子树的高度
    int hl = 0, hr = 0;
    while (l != null) {
        l = l.left;
        hl++;
    }
    while (r != null) {
        r = r.right;
        hr++;
    }
    // 如果左右子树的高度相同，则是一棵满二叉树
    if (hl == hr) {
        return (int)Math.pow(2, hl) - 1;
    }
    // 如果左右高度不同，则按照普通二叉树的逻辑计算
    return 1 + countNodes(root.left) + countNodes(root.right);
}

结合刚才针对满二叉树和普通二叉树的算法，上面这段代码应该不难理解，就是一个结合版，但是其中降低时间复杂度的技巧是非常微妙的。

复杂度分析

开头说了，这个算法的时间复杂度是 O(logNlogN)，这是怎么算出来的呢？直觉感觉好像最坏情况下是 O(NlogN) 吧，因为之前的 while 需要 logN 的时间，最后要 O(N) 的时间向左右子树递归：

1
return 1 + countNodes(root.left) + countNodes(root.right);

关键点在于，这两个递归只有一个会真的递归下去，另一个一定会触发hl == hr而立即返回，不会递归下去。

为什么呢？原因如下：

一棵完全二叉树的两棵子树，至少有一棵是满二叉树：

看图就明显了吧，由于完全二叉树的性质，其子树一定有一棵是满的，所以一定会触发hl == hr，只消耗 O(logN) 的复杂度而不会继续递归。

综上，算法的递归深度就是树的高度 O(logN)，每次递归所花费的时间就是 while 循环，需要 O(logN)，所以总体的时间复杂度是 O(logN*logN)。所以说，「完全二叉树」这个概念还是有它存在的原因的，不仅适用于数组实现二叉堆，而且连计算节点总数这种看起来简单的操作都有高效的算法实现。

如何使用单调栈解题

单调栈实际上就是栈，只是利⽤了⼀些巧妙的逻辑，使得每次新元素⼊栈 后，栈内的元素都保持有序（单调递增或单调递减）。听起来有点像堆（heap）？不是的，单调栈⽤途不太⼴泛，只处理⼀种典型 的问题，叫做 Next Greater Element。本⽂⽤讲解单调队列的算法模版解决 这类问题，并且探讨处理「循环数组」的策略。

题目

⾸先，讲解 Next Greater Number 的原始问题：给你⼀个数组，返回⼀个等 ⻓的数组，对应索引存储着下⼀个更⼤元素，如果没有更⼤的元素，就存 -1。不好⽤语⾔解释清楚，直接上⼀个例⼦：

给你⼀个数组 [2,1,2,4,3]，你返回数组 [4,2,4,-1,-1]。

解释：第⼀个 2 后⾯⽐ 2 ⼤的数是 4; 1 后⾯⽐ 1 ⼤的数是 2；第⼆个 2 后⾯ ⽐ 2 ⼤的数是 4; 4 后⾯没有⽐ 4 ⼤的数，填 -1；3 后⾯没有⽐ 3 ⼤的数，填 -1。这道题的暴⼒解法很好想到，就是对每个元素后⾯都进⾏扫描，找到第⼀个 更⼤的元素就⾏了。但是暴⼒解法的时间复杂度是 O(n^2)。

解法

这个问题可以这样抽象思考：把数组的元素想象成并列站⽴的⼈，元素⼤⼩ 想象成⼈的⾝⾼。这些⼈⾯对你站成⼀列，如何求元素「2」的 Next Greater Number 呢？很简单，如果能够看到元素「2」，那么他后⾯可⻅的第⼀个 ⼈就是「2」的 Next Greater Number，因为⽐「2」⼩的元素⾝⾼不够，都被「2」挡住了，第⼀个露出来的就是答案。

这个情景很好理解吧？带着这个抽象的情景，先来看下代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
vector<int> nextGreaterElement(vector<int>& nums) { 
    vector<int> ans(nums.size()); 
    // 存放答案的数组 
    stack<int> s; 
    for (int i = nums.size() - 1; i >= 0; i--) { 
        // 倒着往栈⾥放 
        while (!s.empty() && s.top() <= nums[i]) { 
            // 判定个⼦⾼矮 
            s.pop(); // 矮个起开，反正也被挡着了。。。 
        }
        ans[i] = s.empty() ? -1 : s.top(); // 这个元素⾝后的第⼀个⾼个 
        s.push(nums[i]); 
        // 进队，接受之后的⾝⾼判定吧！ 
    }
    return ans; 
}

这就是单调队列解决问题的模板。for 循环要从后往前扫描元素，因为我们 借助的是栈的结构，倒着⼊栈，其实是正着出栈。while 循环是把两个“⾼ 个”元素之间的元素排除，因为他们的存在没有意义，前⾯挡着个“更⾼”的 元素，所以他们不可能被作为后续进来的元素的 Next Great Number 了。 这个算法的时间复杂度不是那么直观，如果你看到 for 循环嵌套 while 循 环，可能认为这个算法的复杂度也是 O(n^2)，但是实际上这个算法的复杂 度只有 O(n)

时间复杂度

分析它的时间复杂度，要从整体来看：总共有 n 个元素，每个元素都被 push ⼊栈了⼀次，⽽最多会被 pop ⼀次，没有任何冗余操作。所以总的计 算规模是和元素规模 n 成正⽐的，也就是 O(n) 的复杂度。

给你⼀个数组 T = [73, 74, 75, 71, 69, 72, 76, 73]，这个数组存放的是近⼏天 的天⽓⽓温（这⽓温是铁板烧？不是的，这⾥⽤的华⽒度）。你返回⼀个数 组，计算：对于每⼀天，你还要⾄少等多少天才能等到⼀个更暖和的⽓温； 如果等不到那⼀天，填 0 。

举例：给你 T = [73, 74, 75, 71, 69, 72, 76, 73]，你返回 [1, 1, 4, 2, 1, 1, 0, 0]。

解释：第⼀天 73 华⽒度，第⼆天 74 华⽒度，⽐ 73 ⼤，所以对于第⼀天， 只要等⼀天就能等到⼀个更暖和的⽓温。后⾯的同理。 你已经对 Next Greater Number 类型问题有些敏感了，这个问题本质上也是 找 Next Greater Number，只不过现在不是问你 Next Greater Number 是多 少，⽽是问你当前距离 Next Greater Number 的距离⽽已。 相同类型的问题，相同的思路，直接调⽤单调栈的算法模板，稍作改动就可 以啦，直接上代码把

1
2
3
4
5
6
7
8
9
10
11
12
13
14
vector<int> dailyTemperatures(vector<int>& T) { 
    vector<int> ans(T.size()); 
    stack<int> s; // 这⾥放元素索引，⽽不是元素 
    for (int i = T.size() - 1; i >= 0; i--) { 
        while (!s.empty() && T[s.top()] <= T[i]) { 
            s.pop(); 
        }
        ans[i] = s.empty() ? 0 : (s.top() - i); 
        // 得到索引间距 
        s.push(i); 
        // 加⼊索引，⽽不是元素 
    }
    return ans; 
}

扩展问题：循环数组

单调栈讲解完毕。下⾯开始另⼀个重点：如何处理「循环数组」。

同样是 Next Greater Number，现在假设给你的数组是个环形的，如何处理？

给你⼀个数组 [2,1,2,4,3]，你返回数组 [4,2,4,-1,4]。拥有了环形属性，最后 ⼀个元素 3 绕了⼀圈后找到了⽐⾃⼰⼤的元素 4 。

⾸先，计算机的内存都是线性的，没有真正意义上的环形数组，但是我们可 以模拟出环形数组的效果，⼀般是通过 % 运算符求模（余数），获得环形特效

1
2
3
4
5
6
int[] arr = {1,2,3,4,5}; 
int n = arr.length, index = 0; 
while (true) { 
    print(arr[index % n]); 
    index++; 
}

回到 Next Greater Number 的问题，增加了环形属性后，问题的难点在于：

这个 Next 的意义不仅仅是当前元素的右边了，有可能出现在当前元素的左 边（如上例）。

明确问题，问题就已经解决了⼀半了。我们可以考虑这样的思路：将原始数 组“翻倍”，就是在后⾯再接⼀个原始数组，这样的话，按照之前“⽐⾝⾼”的 流程，每个元素不仅可以⽐较⾃⼰右边的元素，⽽且也可以和左边的元素⽐ 较了

怎么实现呢？你当然可以把这个双倍⻓度的数组构造出来，然后套⽤算法模 板。但是，我们可以不⽤构造新数组，⽽是利⽤循环数组的技巧来模拟。直 接看代码吧： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
vector<int> nextGreaterElements(vector<int>& nums) { 
    int n = nums.size(); 
    vector<int> res(n); 
    // 存放结果 
    stack<int> s; 
    // 假装这个数组⻓度翻倍了 
    for (int i = 2 * n - 1; i >= 0; i--) { 
        while (!s.empty() && s.top() <= nums[i % n]) 
            s.pop(); 
        res[i % n] = s.empty() ? -1 : s.top(); 
        s.push(nums[i % n]); 
    }
    return res; 
}

利用单调队列解题

前⽂讲了⼀种特殊的数据结构「单调栈」monotonic stack，解决了⼀类问题 「Next Greater Number」，本⽂写⼀个类似的数据结构「单调队列」。 也许这种数据结构的名字你没听过，其实没啥难的，就是⼀个「队列」，只 是使⽤了⼀点巧妙的⽅法，使得队列中的元素单调递增（或递减）。这个数 据结构有什么⽤？可以解决滑动窗⼝的⼀系列问题

题目

给定一个数组nums，有一个大小为k的滑动窗口从数组的最左侧移动到数组的最右侧；你只可以看到在滑动窗口k内的数字，滑动窗口每次只向右移动一位，返回滑动窗口最大值。

二叉堆详解

⼆叉堆（Binary Heap）没什么神秘，性质⽐⼆叉搜索树 BST 还简单。其主 要操作就两个， sink （下沉）和 swim （上浮），⽤以维护⼆叉堆的性 质。其主要应⽤有两个，⾸先是⼀种排序⽅法「堆排序」，第⼆是⼀种很有 ⽤的数据结构「优先级队列」。

本⽂就以实现优先级队列（Priority Queue）为例，通过图⽚和⼈类的语⾔来 描述⼀下⼆叉堆怎么运作的

概述

⼆叉堆其实就是⼀种特殊的⼆叉树（完全⼆叉树），只不过存储在数 组⾥。⼀般的链表⼆叉树，我们操作节点的指针，⽽在数组⾥，我们把数组 索引作为指针： 

1
2
3
4
5
6
7
8
9
10
11
12
// ⽗节点的索引 
int parent(int root) { 
    return root / 2; 
}
// 左孩⼦的索引 
int left(int root) { 
    return root * 2; 
}
// 右孩⼦的索引 
int right(int root) { 
    return root * 2 + 1; 
}

画个图你⽴即就能理解了，注意数组的第⼀个索引 0 空着不⽤，二叉堆

PS：因为数组索引是数组，为了⽅便区分，将字符作为数组元素。

你看到了，把 arr[1] 作为整棵树的根的话，每个节点的⽗节点和左右孩⼦的 索引都可以通过简单的运算得到，这就是⼆叉堆设计的⼀个巧妙之处。为了 ⽅便讲解，下⾯都会画的图都是⼆叉树结构，相信你能把树和数组对应起 来

⼆叉堆还分为最⼤堆和最⼩堆。最⼤堆的性质是：每个节点都⼤于等于它的 两个⼦节点。类似的，最⼩堆的性质是：每个节点都⼩于等于它的⼦节点。 两种堆核⼼思路都是⼀样的，本⽂以最⼤堆为例讲解。 对于⼀个最⼤堆，根据其性质，显然堆顶，也就是 arr[1] ⼀定是所有元素中 最⼤的元素。

优先级队列

优先级队列这种数据结构有⼀个很有⽤的功能，你插⼊或者删除元素的时 候，元素会⾃动排序，这底层的原理就是⼆叉堆的操作。

数据结构的功能⽆⾮增删查该，优先级队列有两个主要 API，分别是 insert 插⼊⼀个元素和 delMax 删除最⼤元素（如果底层⽤最⼩堆，那么 就是 delMin ）。

下⾯我们实现⼀个简化的优先级队列，先看下代码框架： PS：为了清晰起⻅，这⾥⽤到 Java 的泛型， Key 可以是任何⼀种可⽐较⼤ ⼩的数据类型，你可以认为它是 int、char 等。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
public class MaxPQ 
    <Key extends Comparable<Key>> { 
    // 存储元素的数组 
    private Key[] pq; 
    // 当前 Priority Queue 中的元素个数 
    private int N = 0; public MaxPQ(int cap) { 
        // 索引 0 不⽤，所以多分配⼀个空间 
        pq = (Key[]) new Comparable[cap + 1]; 
    }
    
    /* 返回当前队列中最⼤元素 */ 
    public Key max() { 
        return pq[1]; 
    }
    /* 插⼊元素 e */ 
    public void insert(Key e) {...} 
    
    /* 删除并返回当前队列中最⼤元素 */ 
    public Key delMax() {...} 
   
    /* 上浮第 k 个元素，以维护最⼤堆性质 */ 
    private void swim(int k) {...} 
    
    /* 下沉第 k 个元素，以维护最⼤堆性质 */ 
    private void sink(int k) {...}
    
    /* 交换数组的两个元素 */ 
    private void exch(int i, int j) { 
        Key temp = pq[i]; 
        pq[i] = pq[j]; 
        pq[j] = temp; 
    }
    
    /* pq[i] 是否⽐ pq[j] ⼩？ */ 
    private boolean less(int i, int j) { 
        return pq[i].compareTo(pq[j]) < 0; 
    }
    /* 还有 left, right, parent 三个⽅法 */ 
}

空出来的四个⽅法是⼆叉堆和优先级队列的奥妙所在，下⾯⽤图⽂来逐个理解

swim和sink

为什么要有上浮 swim 和下沉 sink 的操作呢？为了维护堆结构。 我们要讲的是最⼤堆，每个节点都⽐它的两个⼦节点⼤，但是在插⼊元素和 删除元素时，难免破坏堆的性质，这就需要通过这两个操作来恢复堆的性质了。

对于最⼤堆，会破坏堆性质的有有两种情况：

1、 如果某个节点 A ⽐它的⼦节点（中的⼀个）⼩，那么 A 就不配做⽗节点，应该下去，下⾯那个更⼤的节点上来做⽗节点，这就是对 A 进⾏ 下沉。

2、 如果某个节点 A ⽐它的⽗节点⼤，那么 A 不应该做⼦节点，应该把⽗ 节点换下来，⾃⼰去做⽗节点，这就是对 A 的上浮。

当然，错位的节点 A 可能要上浮（或下沉）很多次，才能到达正确的位 置，恢复堆的性质。所以代码中肯定有⼀个 while 循环。

细⼼的读者也许会问，这两个操作不是互逆吗，所以上浮的操作⼀定能⽤下 沉来完成，为什么我还要费劲写两个⽅法？ 是的，操作是互逆等价的，但是最终我们的操作只会在堆底和堆顶进⾏（等 会讲原因），显然堆底的「错位」元素需要上浮，堆顶的「错位」元素需要 下沉

上浮的代码实现： 

1
2
3
4
5
6
7
8
9
private void swim(int k) { 
    // 如果浮到堆顶，就不能再上浮了 
    while (k > 1 && less(parent(k), k)) { 
        // 如果第 k 个元素⽐上层⼤ 
        // 将 k 换上去 
        exch(parent(k), k); 
        k = parent(k); 
    } 
}

下沉的代码实现： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
private void sink(int k) { 
    // 如果沉到堆底，就沉不下去了 
    while (left(k) <= N) { 
        // 先假设左边节点较⼤ 
        int older = left(k); 
        // 如果右边节点存在，⽐⼀下⼤⼩ 
        if (right(k) <= N && less(older, right(k))) 
            older = right(k); 
        // 结点 k ⽐俩孩⼦都⼤，就不必下沉了 
        if (less(older, k)) break;
        // 否则，不符合最⼤堆的结构，下沉 k 结点 
        exch(k, older); 
        k = older; 
    } 
}

⾄此，⼆叉堆的主要操作就讲完了，⼀点都不难吧，代码加起来也就⼗⾏。 明⽩了 sink 和 swim 的⾏为，下⾯就可以实现优先级队列了

实现 delMax 和 insert

这两个⽅法就是建⽴在 swim 和 sink 上的。 insert ⽅法先把要插⼊的元素添加到堆底的最后，然后让其上浮到正确位 置。

1
2
3
4
5
6
7
public void insert(Key e) { 
    N++; 
    // 先把新元素加到最后 
    pq[N] = e; 
    // 然后让它上浮到正确的位置 
    swim(N); 
}

delMax ⽅法先把堆顶元素 A 和堆底最后的元素 B 对调，然后删除 A**，最** 后让 B 下沉到正确位置。

1
2
3
4
5
6
7
8
9
10
11
public Key delMax() { 
    // 最⼤堆的堆顶就是最⼤元素 
    Key max = pq[1]; 
    // 把这个最⼤元素换到最后，删除之 
    exch(1, N);
    pq[N] = null; 
    N--; 
    // 让 pq[1] 下沉到正确位置 
    sink(1); 
    return max; 
}

⾄此，⼀个优先级队列就实现了，插⼊和删除元素的时间复杂度为 O(logK) ， K 为当前⼆叉堆（优先级队列）中的元素总数。因为我们时间 复杂度主要花费在 sink 或者 swim 上，⽽不管上浮还是下沉，最多也就 树（堆）的⾼度，也就是 log 级别

总结

⼆叉堆就是⼀种完全⼆叉树，所以适合存储在数组中，⽽且⼆叉堆拥有⼀些 特殊性质。

⼆叉堆的操作很简单，主要就是上浮和下沉，来维护堆的性质（堆有序）， 核⼼代码也就⼗⾏。

优先级队列是基于⼆叉堆实现的，主要操作是插⼊和删除。插⼊是先插到最 后，然后上浮到正确位置；删除是调换位置后再删除，然后下沉到正确位 置。核⼼代码也就⼗⾏。

也许这就是数据结构的威⼒，简单的操作就能实现巧妙的功能，真⼼佩服发明⼆叉堆算法的⼈！

发表于 更新于

双指针技巧详解

主要分为两类：1、快慢指针；2、左右指针；前者主要解决链表中的问题，比如典型的判定链表中是否包含环；后者主要解决数组（或字符串）中的问题，比如：二分查找。

链表、子串、数组的题目，一般都需要用到双指针技巧。

链表指针数组题，用双指针别犹豫。

双指针家三兄弟，各个都是万人迷。

快慢指针最神奇，链表操作无压力。

归并排序找中点，链表成环搞判定。

左右指针最常见，左右两端相向行。

反转数组要靠它，二分搜索是弟弟。

滑动窗口老猛男，子串问题全靠它。

左右指针滑窗口，一前一后齐头进。

快慢指针的用法

快慢指针一般都初始化指向链表的头节点head，前进时快指针fast在前，慢指针slow在后，从而巧妙解决链表中问题。

判定链表中是否有环

单链表的特点是每个节点只知道下⼀个节点，所以⼀个指针的话⽆法判断链 表中是否含有环的。 如果链表中不含环，那么这个指针最终会遇到空指针 null 表⽰链表到头 了，这还好说，可以判断该链表不含环。但是如果链表中含有环，那么这个指针就会陷⼊死循环，因为环形数组中没 有 null 指针作为尾部节点。

经典解法就是⽤两个指针，⼀个跑得快，⼀个跑得慢。如果不含有环，跑得 快的那个指针最终会遇到 null，说明链表不含环；如果含有环，快指针最终 会超慢指针⼀圈，和慢指针相遇，说明链表含有环。

1
2
3
4
5
6
7
8
9
10
boolean hasCycle(ListNode head) { 
    ListNode fast, slow; 
    fast = slow = head; 
    while (fast != null && fast.next != null) { 
        fast = fast.next.next; 
        slow = slow.next; 
        if (fast == slow) return true; 
    }
    return false; 
}

已知链表中有环，返回其起始位置

可以看到，当快慢指针相遇时，让其中任⼀个指针指向头节点，然后让它俩 以相同速度前进，再次相遇时所在的节点位置就是环开始的位置。

第⼀次相遇时，假设慢指针 slow ⾛了 k 步，那么快指针 fast ⼀定⾛了 2k 步，也就是说⽐ slow 多⾛了 k 步（也就是环的⻓度）。设相遇点距环的起点的距离为 m，那么环的起点距头结点 head 的距离为 k - m，也就是说如果从 head 前进 k - m 步就能到达环起点。 巧的是，如果从相遇点继续前进 k - m 步，也恰好到达环起点。 所以，只要我们把快慢指针中的任⼀个重新指向 head，然后两个指针同速 前进，k - m 步后就会相遇，相遇之处就是环的起点了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
ListNode detectCycle(ListNode head) { 
    ListNode fast, slow; 
    fast = slow = head; 
    while (fast != null && fast.next != null) { 
        fast = fast.next.next; 
        slow = slow.next; 
        if (fast == slow) 
            break; 
    }// 上⾯的代码类似 hasCycle 函数
        slow = head; 
    while (slow != fast) { 
        fast = fast.next; 
        slow = slow.next; 
    }
    return slow; 
}

寻找链表的中点

类似上⾯的思路，我们还可以让快指针⼀次前进两步，慢指针⼀次前进⼀ 步，当快指针到达链表尽头时，慢指针就处于链表的中间位置。当链表的⻓度是奇数时，slow 恰巧停在中点位置；如果⻓度是偶数，slow 最终的位置是中间偏右。

寻找链表中点的⼀个重要作⽤是对链表进⾏归并排序。 回想数组的归并排序：求中点索引递归地把数组⼆分，最后合并两个有序数 组。对于链表，合并两个有序链表是很简单的，难点就在于⼆分。 但是现在你学会了找到链表的中点，就能实现链表的⼆分了。

1
2
3
4
5
while (fast != null && fast.next != null) { 
    fast = fast.next.next;
    slow = slow.next; 
}// slow 就在中间位置 
return slow;

寻找链表的倒数第k个元素

我们的思路还是使⽤快慢指针，让快指针先⾛ k 步，然后快慢指针开始同速 前进。这样当快指针⾛到链表末尾 null 时，慢指针所在的位置就是倒数第 k 个链表节点。

1
2
3
4
5
6
7
8
ListNode slow, fast; 
slow = fast = head; 
while (k-- > 0) 
    fast = fast.next; 
while (fast != null) { 
    slow = slow.next; 
    fast = fast.next; }
return slow;

左右指针的常见用法

左右指针在数组中实际是指两个索引值，⼀般初始化为 left = 0, right = nums.length - 1 。

二分查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int binarySearch(int[] nums, int target) { 
    int left = 0; 
    int right = nums.length - 1;
    while(left <= right) { 
        int mid = (right + left) / 2; 
        if(nums[mid] == target) 
            return mid; 
        else if (nums[mid] < target) 
            left = mid + 1; 
        else if (nums[mid] > target) 
            right = mid - 1; 
    }
    return -1; 
}

二数之和

给定一个已经按照升序排列的有序数组，找到两个数使得它们相加之和等于目标数。函数应该返回两个下标值index1和index2。

只要数组有序就应该想到双指针用法，解法类似于二分查找，通过调节left和right来调整sum的大小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int[] twoSum(int[] nums, int target) { 
    int left = 0, right = nums.length - 1; 
    while (left < right) { 
        int sum = nums[left] + nums[right]; 
        if (sum == target) { // 题⽬要求的索引是从 1 开始的
            return new int[]{left + 1, right + 1}; 
        } 
        else if (sum < target) { 
            left++; 
            // 让 sum ⼤⼀点 
        } else if (sum > target) { 
            right--; 
            // 让 sum ⼩⼀点 
        } 
    }
    return new int[]{-1, -1}; 
}

反转数组

1
2
3
4
5
6
7
8
9
10
11
12
void reverse(int[] nums) { 
    int left = 0; 
    int right = nums.length - 1; 
    while (left < right) { 
        // swap(nums[left], nums[right]) 
        int temp = nums[left]; 
        nums[left] = nums[right]; 
        nums[right] = temp; 
        left++; 
        right--; 
    } 
}

滑动窗口算法

滑动窗口是双指针技巧的最高境界，可以解决一大类子字符串匹配的问题，比如：最小覆盖子串、字符串的排列、找到字符串中所有字母异位词、无重复字符的最长子串。其实算法的技巧思路特别简单，即维护一个窗口，不断滑动并更新答案。

1
2
3
4
5
6
7
8
9
10
11
12
int left = 0, right = 0;
while (right < s.size()) {
    // 增⼤窗⼝ 
    window.add(s[right]); 
    right++; 
    
    while (window needs shrink) { 
        // 缩⼩窗⼝ 
        window.remove(s[left]); 
        left++; 
    } 
}

这个算法技巧的时间复杂度是 O(N)，⽐字符串暴⼒算法要⾼效得多。 其实困扰⼤家的，不是算法的思路，⽽是各种细节问题。⽐如说如何向窗⼝ 中添加新元素，如何缩⼩窗⼝，在窗⼝滑动的哪个阶段更新结果。即便你明 ⽩了这些细节，也容易出 bug，找 bug 还不知道怎么找，真的挺让⼈⼼烦 的。

所以今天我就写⼀套滑动窗⼝算法的代码框架，我连再哪⾥做输出 debug 都给你写好了，以后遇到相关的问题，你就默写出来如下框架然后改三个地 ⽅就⾏，还不会出 bug： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/* 滑动窗口算法框架 */
void slidingWindow(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;

    int left = 0, right = 0;
    int valid = 0; 
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];
        // 右移窗口
        right++;
        // 进行窗口内数据的一系列更新
        ...

        /*** debug 输出的位置 ***/
        printf("window: [%d, %d)\n", left, right);
        /********************/

        // 判断左侧窗口是否要收缩
        while (window needs shrink) {
            // d 是将移出窗口的字符
            char d = s[left];
            // 左移窗口
            left++;
            // 进行窗口内数据的一系列更新
            ...
        }
    }
}

而且，这两个...处的操作分别是右移和左移窗口更新操作，等会你会发现它们操作是完全对称的。本文代码为 C++ 实现，不会用到什么编程方面的奇技淫巧，但是还是简单介绍一下一些用到的数据结构，以免有的读者因为语言的细节问题阻碍对算法思想的理解：

unordered_map就是哈希表（字典），它的一个方法count(key)相当于 Java 的containsKey(key)可以判断键 key 是否存在。可以使用方括号访问键对应的值map[key]。需要注意的是，如果该key不存在，C++ 会自动创建这个 key，并把map[key]赋值为 0。所以代码中多次出现的map[key]++相当于 Java 的map.put(key, map.getOrDefault(key, 0) + 1)。

最小覆盖子串

题目：给你一个字符串S、字符串T，请在字符串S中找出：包含T所有字母的最小子串。

就是说要在S(source) 中找到包含T(target) 中全部字母的一个子串，且这个子串一定是所有可能子串中最短的。

如果我们使用暴力解法，代码大概是这样的：

1
2
3
4
for (int i = 0; i < s.size(); i++)
    for (int j = i + 1; j < s.size(); j++)
        if s[i:j] 包含 t 的所有字母:
            更新答案

而滑动窗口的思路是这样的：

1、我们在字符串S中使用双指针中的左右指针技巧，初始化left = right = 0，把索引左闭右开区间[left, right)称为一个「窗口」。

2、我们先不断地增加right指针扩大窗口[left, right)，直到窗口中的字符串符合要求（包含了T中的所有字符）。

3、此时，我们停止增加right，转而不断增加left指针缩小窗口[left, right)，直到窗口中的字符串不再符合要求（不包含T中的所有字符了）。同时，每次增加left，我们都要更新一轮结果。

4、重复第 2 和第 3 步，直到right到达字符串S的尽头

这个思路其实也不难，第 2 步相当于在寻找一个「可行解」，然后第 3 步在优化这个「可行解」，最终找到最优解，也就是最短的覆盖子串。左右指针轮流前进，窗口大小增增减减，窗口不断向右滑动，这就是「滑动窗口」这个名字的来历。下面画图理解一下，needs和window相当于计数器，分别记录T中字符出现次数和「窗口」中的相应字符的出现次数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
//首先，初始化window和need两个哈希表，记录窗口中的字符和需要凑齐的字符：
unordered_map<char, int> need, window;
for (char c : t) need[c]++;//为每个键值赋值

//然后，使用left和right变量初始化窗口的两端，不要忘了，区间[left, right)是左闭右开的，所以初始情况下窗口没有包含任何元素：
int left = 0, right = 0;
int valid = 0; 
while (right < s.size()) {
    // 开始滑动
}
//其中valid变量表示窗口中满足need条件的字符个数，如果valid和need.size的大小相同，则说明窗口已满足条件，已经完全覆盖了串T。
//现在开始套模板，只需要思考以下四个问题：
//1、当移动right扩大窗口，即加入字符时，应该更新哪些数据？
//2、什么条件下，窗口应该暂停扩大，开始移动left缩小窗口？
//3、当移动left缩小窗口，即移出字符时，应该更新哪些数据？
//4、我们要的结果应该在扩大窗口时还是缩小窗口时进行更新？

//如果一个字符进入窗口，应该增加window计数器；如果一个字符将移出窗口的时候，应该减少window计数器；当valid满足need时应该收缩窗口；应该在收缩窗口的时候更新最终结果。

string minWindow(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;

    int left = 0, right = 0;
    int valid = 0;
    // 记录最小覆盖子串的起始索引及长度
    int start = 0, len = INT_MAX;
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];
        // 右移窗口
        right++;
        // 进行窗口内数据的一系列更新
        if (need.count(c)) {
            window[c]++;
            if (window[c] == need[c])
                valid++;
        }

        // 判断左侧窗口是否要收缩
        while (valid == need.size()) {
            // 在这里更新最小覆盖子串
            if (right - left < len) {
                start = left;
                len = right - left;
            }
            // d 是将移出窗口的字符
            char d = s[left];
            // 左移窗口
            left++;
            // 进行窗口内数据的一系列更新
            if (need.count(d)) {
                if (window[d] == need[d])
                    valid--;
                window[d]--;
            }                    
        }
    }
    // 返回最小覆盖子串
    return len == INT_MAX ?
        "" : s.substr(start, len);
}

需要注意的是，当我们发现某个字符在window的数量满足了need的需要，就要更新valid，表示有一个字符已经满足要求。而且，你能发现，两次对窗口内数据的更新操作是完全对称的。

当valid == need.size()时，说明T中所有字符已经被覆盖，已经得到一个可行的覆盖子串，现在应该开始收缩窗口了，以便得到「最小覆盖子串」。移动left收缩窗口时，窗口内的字符都是可行解，所以应该在收缩窗口的阶段进行最小覆盖子串的更新，以便从可行解中找到长度最短的最终结果。

至此，应该可以完全理解这套框架了，滑动窗口算法又不难，就是细节问题让人烦得很。以后遇到滑动窗口算法，你就按照这框架写代码，保准没有 bug，还省事儿。

字符串排列

题目：给定两个字符串S1、S2，写一个函数来判断S2是否包含S1的序列；即第一个字符串的排列之一是第二个字符串的子串

这种题目，是明显的滑动窗口算法，相当给你一个S和一个T，请问你S中是否存在一个子串，包含T中所有字符且不包含其他字符？首先，先复制粘贴之前的算法框架代码，然后明确刚才提出的 4 个问题，即可写出这道题的答案：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
// 判断 s 中是否存在 t 的排列
bool checkInclusion(string t, string s) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;

    int left = 0, right = 0;
    int valid = 0;
    while (right < s.size()) {
        char c = s[right];
        right++;
        // 进行窗口内数据的一系列更新
        if (need.count(c)) {
            window[c]++;
            if (window[c] == need[c])
                valid++;
        }

        // 判断左侧窗口是否要收缩
        while (right - left >= t.size()) {
            // 在这里判断是否找到了合法的子串
            if (valid == need.size())
                return true;
            char d = s[left];
            left++;
            // 进行窗口内数据的一系列更新
            if (need.count(d)) {
                if (window[d] == need[d])
                    valid--;
                window[d]--;
            }
        }
    }
    // 未找到符合条件的子串
    return false;
}

对于这道题的解法代码，基本上和最小覆盖子串一模一样，只需要改变两个地方：

1、本题移动left缩小窗口的时机是窗口大小大于t.size()时，因为排列嘛，显然长度应该是一样的。

2、当发现valid == need.size()时，就说明窗口中就是一个合法的排列，所以立即返回true。

至于如何处理窗口的扩大和缩小，和最小覆盖子串完全相同。

找所有字母异位词

给定一个字符串s和非空字符串p，找到s中所有是p的字母异位词的子串，返回这些子串的起始索引。（字母异位词指字母相同，但排列不同的字符串；不考虑答案输出的顺序）

呵呵，这个所谓的字母异位词，不就是排列吗，搞个高端的说法就能糊弄人了吗？相当于，输入一个串S，一个串T，找到S中所有T的排列，返回它们的起始索引。直接默写一下框架，明确刚才讲的 4 个问题，即可秒杀这道题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
vector<int> findAnagrams(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;

    int left = 0, right = 0;
    int valid = 0;
    vector<int> res; // 记录结果
    while (right < s.size()) {
        char c = s[right];
        right++;
        // 进行窗口内数据的一系列更新
        if (need.count(c)) {
            window[c]++;
            if (window[c] == need[c]) 
                valid++;
        }
        // 判断左侧窗口是否要收缩
        while (right - left >= t.size()) {
            // 当窗口符合条件时，把起始索引加入 res
            if (valid == need.size())
                res.push_back(left);
            char d = s[left];
            left++;
            // 进行窗口内数据的一系列更新
            if (need.count(d)) {
                if (window[d] == need[d])
                    valid--;
                window[d]--;
            }
        }
    }
    return res;
}

跟寻找字符串的排列一样，只是找到一个合法异位词（排列）之后将起始索引加入res即可

最长无重复子串

题目：给定一个字符串，找出其中不含有重复重复字符的的最长子串的长度。

这个题终于有了点新意，不是一套框架就出答案，不过反而更简单了，稍微改一改框架就行了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
int lengthOfLongestSubstring(string s) {
    unordered_map<char, int> window;

    int left = 0, right = 0;
    int res = 0; // 记录结果
    while (right < s.size()) {
        char c = s[right];
        right++;
        // 进行窗口内数据的一系列更新
        window[c]++;
        // 判断左侧窗口是否要收缩
        while (window[c] > 1) {
            char d = s[left];
            left++;
            // 进行窗口内数据的一系列更新
            window[d]--;
        }
        // 在这里更新答案
        res = max(res, right - left);
    }
    return res;
}

这就是变简单了，连need和valid都不需要，而且更新窗口内数据也只需要简单的更新计数器window即可。

当window[c]值大于 1 时，说明窗口中存在重复字符，不符合条件，就该移动left缩小窗口了嘛。唯一需要注意的是，在哪里更新结果res呢？我们要的是最长无重复子串，哪一个阶段可以保证窗口中的字符串是没有重复的呢？

这里和之前不一样，**要在收缩窗口完成后更新res**，因为窗口收缩的 while 条件是存在重复元素，换句话说收缩完成后一定保证窗口中没有重复嘛。

twoSum问题的核心思想

第一题

这个问题的最基本形式是这样：给你⼀个数组和⼀个整数 target ，可以保 证数组中存在两个数的和为 target ，请你返回这两个数的索引。这个问题如何解决呢？⾸先最简单粗暴的办法当然是穷举了：

1
2
3
4
5
6
7
8
int[] twoSum(int[] nums, int target) { 
    for (int i = 0; i < nums.length; i++) 
        for (int j = i + 1; j < nums.length; j++) 
            if (nums[j] == target - nums[i]) 
                return new int[] { i, j }; 
    // 不存在这么两个数 
    return new int[] {-1, -1}; 
}

这个解法⾮常直接，时间复杂度 O(N^2)，空间复杂度 O(1)。 可以通过⼀个哈希表减少时间复杂度：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int[] twoSum(int[] nums, int target) { 
    int n = nums.length; 
    index<Integer, Integer> 
        index = new HashMap<>();
    // 构造⼀个哈希表：元素映射到相应的索引 
    for (int i = 0; i < n; i++) 
        index.put(nums[i], i); 
    for (int i = 0; i < n; i++) { 
        int other = target - nums[i]; 
        // 如果 other 存在且不是 nums[i] 本⾝ 
        if (index.containsKey(other) && index.get(other) != i) 
            return new int[] {i, index.get(other)}; 
    }
    return new int[] {-1, -1};
}

这样，由于哈希表的查询时间为 O(1)，算法的时间复杂度降低到 O(N)，但 是需要 O(N) 的空间复杂度来存储哈希表。不过综合来看，是要⽐暴⼒解法 ⾼效的。

我觉得 Two Sum 系列问题就是想教我们如何使⽤哈希表处理问题。我们接 着往后看。

第二题

这⾥我们稍微修改⼀下上⾯的问题。我们设计⼀个类，拥有两个 API： 

1
2
3
4
5
6
class TwoSum { 
    // 向数据结构中添加⼀个数 number 
    public void add(int number); 
    // 寻找当前数据结构中是否存在两个数的和为 value 
    public boolean find(int value); 
}

如何实现这两个 API 呢，我们可以仿照上⼀道题⽬，使⽤⼀个哈希表辅助 find ⽅法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class TwoSum { 
    Map<Integer, Integer> freq = new HashMap<>();
    public void add(int number) { 
        // 记录 number 出现的次数 
        freq.put(number, freq.getOrDefault(number, 0) + 1); 
    }
    
    public boolean find(int value) { 
        for (Integer key : freq.keySet()) { 
            int other = value - key; 
            // 情况⼀ 
            if (other == key && freq.get(key) > 1) 
                return true;
            // 情况⼆ 
            if (other != key && freq.containsKey(other)) 
                return true; 
        }
        return false; 
    } 
}

进⾏ find 的时候有两种情况，举个例⼦：

情况⼀： add 了 [3,3,2,5] 之后，执⾏ find(6) ，由于 3 出现了两次，3 + 3 = 6，所以返回 true。

情况⼆： add 了 [3,3,2,5] 之后，执⾏ find(7) ，那么 key 为 2， other 为 5 时算法可以返回 true。

除了上述两种情况外， find 只能返回 false 了。

对于这个解法的时间复杂度呢， add ⽅法是 O(1)， find ⽅法是 O(N)，空 间复杂度为 O(N)，和上⼀道题⽬⽐较类似。但是对于 API 的设计，是需要考虑现实情况的。⽐如说，我们设计的这个 类，使⽤ find ⽅法⾮常频繁，那么每次都要 O(N) 的时间，岂不是很浪费 费时间吗？对于这种情况，我们是否可以做些优化呢？

是的，对于频繁使⽤ find ⽅法的场景，我们可以进⾏优化。我们可以参 考上⼀道题⽬的暴⼒解法，借助哈希集合来针对性优化 find ⽅法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class TwoSum {
    Set<Integer> sum = new HashSet<>(); 
    List<Integer> nums = new ArrayList<>(); 
    
    public void add(int number) { 
        // 记录所有可能组成的和 
        for (int n : nums) 
            sum.add(n + number); 
        nums.add(number); 
    }
    public boolean find(int value) { 
        return sum.contains(value); 
    } 
}

这样 sum 中就储存了所有加⼊数字可能组成的和，每次 find 只要花费 O(1) 的时间在集合中判断⼀下是否存在就⾏了，显然⾮常适合频繁使⽤ find 的场景。

对于 TwoSum 问题，⼀个难点就是给的数组⽆序。对于⼀个⽆序的数组， 我们似乎什么技巧也没有，只能暴⼒穷举所有可能。

⼀般情况下，我们会⾸先把数组排序再考虑双指针技巧。TwoSum 启发我 们，HashMap 或者 HashSet 也可以帮助我们处理⽆序数组相关的简单问题。 另外，设计的核⼼在于权衡，利⽤不同的数据结构，可以得到⼀些针对性的 加强。

最后，如果 TwoSum I 中给的数组是有序的，应该如何编写算法呢？答案很 简单，前⽂「双指针技巧汇总」写过：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int[] twoSum(int[] nums, int target) { 
    int left = 0, right = nums.length - 1; 
    while (left < right) { 
        int sum = nums[left] + nums[right]; 
        if (sum == target) {
            return new int[]{left, right}; 
        } else if (sum < target) { 
            left++; // 让 sum ⼤⼀点 
        } else if (sum > target) { 
            right--; // 让 sum ⼩⼀点 
        } 
    }
    // 不存在这样两个数 
    return new int[]{-1, -1}; 
}

二分查找详解

⼆分查找并不简单，Knuth ⼤佬（发明 KMP 算法的那位）都说⼆分查找：

思路很简单，细节是魔⿁。很多⼈喜欢拿整型溢出的 bug 说事⼉，但是⼆分 查找真正的坑根本就不是那个细节问题，⽽是在于到底要给 mid 加⼀还是 减⼀，while ⾥到底⽤ <= 还是 < 。

二分搜索诗

管他左侧还右侧，搜索区间定乾坤。

搜索一个元素时，搜索区间两端闭。

while条件带等号，否则需要打补丁。

if相等就返回，其他的事甭操心。

mid必须加减一，因为区间两端闭。

while结束就凉凉，凄凄惨惨返-1。

搜索左右边界时，搜索区间要阐明。

左闭右开最常见，其余逻辑便自明。

while要用小于号，这样才能不漏掉。

if相等别返回，利用mid锁边界。

mid加一或减一？要看区间区间开或闭。

while结束不算完，因为你还没返回。

索引可能出边界，if检查保平安。

二分查找框架

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int binarySearch(int[] nums, int target) { 
    int left = 0, right = ...; 
    while(...) { 
        int mid = left + (right - left) / 2; 
        if (nums[mid] == target) { 
            ... 
        } else if (nums[mid] < target) { 
            left = ... 
        } else if (nums[mid] > target) { 
            right = ... 
        } 
    }
    return ...; 
}

分析⼆分查找的⼀个技巧是：不要出现 else**，⽽是把所有情况⽤** else if 写清 楚，这样可以清楚地展现所有细节。本⽂都会使⽤ else if，旨在讲清楚。

其中 … 标记的部分，就是可能出现细节问题的地⽅，当你⻅到⼀个⼆分 查找的代码时，⾸先注意这⼏个地⽅。后⽂⽤实例分析这些地⽅能有什么样 的变化。

另外声明⼀下，计算 mid 时需要防⽌溢出，代码中 left + (right - left) / 2 就和 (left + right) / 2 的结果相同，但是有效防⽌了 left 和right 太⼤直接相加导致溢出

寻找一个数：基本二分查找

这个场景是最简单的，肯能也是⼤家最熟悉的，即搜索⼀个数，如果存在， 返回其索引，否则返回 -1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int binarySearch(int[] nums, int target) { 
    int left = 0;
    int right = nums.length - 1; // 注意 
    while(left <= right) { 
        int mid = left + (right - left) / 2; 
        if(nums[mid] == target) 
            return mid; 
        else if (nums[mid] < target) 
            left = mid + 1; // 注意 
        else if (nums[mid] > target) 
            right = mid - 1; // 注意 
    }
    return -1; 
}

1**、为什么** while 循环的条件中是 <=**，⽽不是** **<**？

答：因为初始化 right 的赋值是 nums.length - 1 ，即最后⼀个元素的索 引，⽽不是 nums.length 。

这⼆者可能出现在不同功能的⼆分查找中，区别是：前者相当于两端都闭区 间 [left, right] ，后者相当于左闭右开区间 [left, right) ，因为索引⼤⼩为 nums.length 是越界的。

我们这个算法中使⽤的是前者 [left, right] 两端都闭的区间。这个区间

其实就是每次进⾏搜索的区间。

2、什么时候应该停⽌搜索呢？

当然，找到了⽬标值的时候可以终⽌：

if(nums[mid] == target) return mid;

但如果没找到，就需要 while 循环终⽌，然后返回 -1。那 while 循环什么时 候应该终⽌？搜索区间为空的时候应该终⽌，意味着你没得找了，就等于没 找到嘛。

while(left <= right) 的终⽌条件是 left == right + 1 ，写成区间的形式 就是 [right + 1, right] ，或者带个具体的数字进去 [3, 2] ，可⻅这时候 区间为空，

while(left < right) 的终⽌条件是 left == right ，写成区间的形式就是 [left, right] ，或者带个具体的数字进去 [2, 2] ，这时候区间⾮空，还 有⼀个数 2，但此时 while 循环终⽌了。也就是说这区间 [2, 2] 被漏掉 了，索引 2 没有被搜索，如果这时候直接返回 -1 就是错误的。

3**、为什么** left = mid + 1 ， right = mid - 1 ？我看有的代码是 right = mid 或者 left = mid ，没有这些加加减减，到底怎么回事，怎么判断？

答：这也是⼆分查找的⼀个难点，不过只要你能理解前⾯的内容，就能够很 容易判断。

刚才明确了「搜索区间」这个概念，⽽且本算法的搜索区间是两端都闭的， 即 [left, right] 。那么当我们发现索引 mid 不是要找的 target 时，下 ⼀步应该去搜索哪⾥呢？ 当然是去搜索 [left, mid-1] 或者 [mid+1, right] 对不对？因为 mid 已 经搜索过，应该从搜索区间中去除。

4**、此算法有什么缺陷**？

答：⾄此，你应该已经掌握了该算法的所有细节，以及这样处理的原因。但 是，这个算法存在局限性。

⽐如说给你有序数组 nums = [1,2,2,2,3] ， target 为 2，此算法返回的索 引是 2，没错。但是如果我想得到 target 的左侧边界，即索引 1，或者我 想得到 target 的右侧边界，即索引 3，这样的话此算法是⽆法处理的。

寻找左侧边界的⼆分搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int left_bound(int[] nums, int target) { 
    if (nums.length == 0) return -1; 
    int left = 0; 
    int right = nums.length; // 注意 
    while (left < right) { // 注意 
        int mid = (left + right) / 2; 
        if (nums[mid] == target) { 
            right = mid; 
        } else if (nums[mid] < target) { 
            left = mid + 1; 
        } else if (nums[mid] > target) { 
            right = mid; // 注意 
        } 
    }
    return left; 
}

1**、为什么** while 中是 < ⽽不是 <= ?

答：⽤相同的⽅法分析，因为 right = nums.length ⽽不是 nums.length - 1 。因此每次循环的「搜索区间」是 [left, right) 左闭右开。 while(left < right) 终⽌的条件是 left == right ，此时搜索区间 [left, left) 为空，所以可以正确终⽌。

寻找右侧边界的⼆分查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int right_bound(int[] nums, int target) { 
    if (nums.length == 0) return -1; 
    int left = 0, right = nums.length; 
    
    while (left < right) { 
        int mid = (left + right) / 2; 
        if (nums[mid] == target) { 
            left = mid + 1; // 注意 
        } else if (nums[mid] < target) {
            left = mid + 1; 
        } else if (nums[mid] > target) { 
            right = mid; 
        } 
    }return left - 1; // 注意 
}

字符串乘法

对于⽐较⼩的数字，做运算可以直接使⽤编程语⾔提供的运算符，但是如果 相乘的两个因数⾮常⼤，语⾔提供的数据类型可能就会溢出。⼀种替代⽅案 就是，运算数以字符串的形式输⼊，然后模仿我们⼩学学习的乘法算术过程 计算出结果，并且也⽤字符串表⽰。

题目

给定两个以字符串形式表示的非负整数num1、num2，返回num1和num2的乘积，它们的乘积也表示为字符串的形式。

需要注意的是， num1 和 num2 可以⾮常⻓，所以不可以把他们直接转成 整型然后运算，唯⼀的思路就是模仿我们⼿算乘法。

思路

计算 123 × 5 ，再计算 123 × 4 ，最后错⼀位相加。这个流程恐怕⼩学⽣ 都可以熟练完成，但是你是否能把这个运算过程进⼀步机械化，写成⼀套算 法指令让没有任何智商的计算机来执⾏呢？

你看这个简单过程，其中涉及乘法进位，涉及错位相加，还涉及加法进位； ⽽且还有⼀些不易察觉的问题，⽐如说两位数乘以两位数，结果可能是四位 数，也可能是三位数，你怎么想出⼀个标准化的处理⽅式？这就是算法的魅 ⼒，如果没有计算机思维，简单的问题可能都没办法⾃动化处理。

⾸先，我们这种⼿算⽅式还是太「⾼级」了，我们要再「低级」⼀点， 123 × 5 和 123 × 4 的过程还可以进⼀步分解，最后再相加：

现在 123 并不⼤，如果是个很⼤的数字的话，是⽆法直接计算乘积的。我 们可以⽤⼀个数组在底下接收相加结果：

整个计算过程⼤概是这样，有两个指针 *i**，j 在 num1 和 num2 上游⾛，

计算乘积，同时将乘积叠加到 res 的正确位置： 现在还有⼀个关键问题，如何将乘积叠加到 res 的正确位置，或者说，如 何通过 i，j 计算 res 的对应索引呢？ 其实，细⼼观察之后就发现， num1[i] 和 num2[j] 的乘积对应的就是 res[i+j] 和 res[i+j+1] 这两个位置。

明⽩了这⼀点，就可以⽤代码模仿出这个计算过程了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
string multiply(string num1, string num2) { 
    int m = num1.size(), n = num2.size(); 
    // 结果最多为 m + n 位数 
    vector<int> res(m + n, 0); 
    // 从个位数开始逐位相乘 
    for (int i = m - 1; i >= 0; i--) 
        for (int j = n - 1; j >= 0; j--) { 
            int mul = (num1[i]-'0') * (num2[j]-'0'); 
            // 乘积在 res 对应的索引位置 
            int p1 = i + j, p2 = i + j + 1; 
            // 叠加到 res 上 
            int sum = mul + res[p2]; 
            res[p2] = sum % 10; 
            res[p1] += sum / 10; 
        } 
    // 结果前缀可能存的 0（未使⽤的位） 
    int i = 0; 
    while (i < res.size() && res[i] == 0) 
        i++; 
    // 将计算结果转化成字符串 
    string str; 
    for (; i < res.size(); i++) 
        str.push_back('0' + res[i]); 
    return str.size() == 0 ? "0" : str; 
}

总结⼀下，我们习以为常的⼀些思维⽅式，在计算机看来是⾮常难以做到 的。⽐如说我们习惯的算术流程并不复杂，但是如果让你再进⼀步，翻译成 代码逻辑，并不简单。算法需要将计算流程再简化，通过边算边叠加的⽅式 来得到结果。

俗话教育我们，不要陷⼊思维定式，不要程序化，要发散思维，要创新。但 我觉得程序化并不是坏事，可以⼤幅提⾼效率，减⼩失误率。算法不就是⼀ 套程序化的思维吗，只有程序化才能让计算机帮助我们解决复杂问题呀！

前缀和技巧

题目：

算出⼀共有⼏个和为 k 的⼦数组。给定一个整数数组和一个整数k，你需要找到该数组中和为k的连续的子数组的个数。

输入：nums = [1,1,1], k = 2；输出：2，[1,1]与[1,1]为两种不同的情况。

解法思路：

那我把所有⼦数组都穷举出来，算它们的和，看看谁的和等于 k 不就⾏了。 关键是，如何快速得到某个⼦数组的和呢，⽐如说给你⼀个数组 nums ，让 你实现⼀个接⼝ sum(i, j) ，这个接⼝要返回 nums[i..j] 的和，⽽且会被 多次调⽤，你怎么实现这个接⼝呢？

因为接⼝要被多次调⽤，显然不能每次都去遍历 nums[i..j] ，有没有⼀种 快速的⽅法在 O(1) 时间内算出 nums[i..j] 呢？这就需要前缀和技巧了。

什么是前缀和

前缀和的思路是这样的，对于⼀个给定的数组 nums ，我们额外开辟⼀个前 缀和数组进⾏预处理：

1
2
3
4
5
int n = nums.length; // 前缀和数组
int[] preSum = new int[n + 1]; 
preSum[0] = 0; 
for (int i = 0; i < n; i++) 
    preSum[i + 1] = preSum[i] + nums[i];

这个前缀和数组 preSum 的含义也很好理解， preSum[i] 就是 nums[0..i- 1] 的和。那么如果我们想求 nums[i..j] 的和，只需要⼀步操作

preSum[j+1]-preSum[i] 即可，⽽不需要重新去遍历数组了。

回到这个⼦数组问题，我们想求有多少个⼦数组的和为 k，借助前缀和技巧

很容易写出⼀个解法： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int subarraySum(int[] nums, int k) { 
    int n = nums.length; 
    // 构造前缀和 
    int[] sum = new int[n + 1]; 
    sum[0] = 0; 
    for (int i = 0; i < n; i++) 
        sum[i + 1] = sum[i] + nums[i]; 
    int ans = 0; // 穷举所有⼦数组 
    for (int i = 1; i <= n; i++) 
        for (int j = 0; j < i; j++)
            // sum of nums[j..i-1] 
            if (sum[i] - sum[j] == k) 
                ans++; 
    return ans; 
}

这个解法的时间复杂度 O(N^2) 空间复杂度 O(N) ，并不是最优的解法。不 过通过这个解法理解了前缀和数组的⼯作原理之后，可以使⽤⼀些巧妙的办 法把时间复杂度进⼀步降低

优化解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
//前⾯的解法有嵌套的 for 循环：
for (int i = 1; i <= n; i++) 
    for (int j = 0; j < i; j++) 
        if (sum[i] - sum[j] == k) 
            ans++;
//第⼆层 for 循环在⼲嘛呢？翻译⼀下就是，在计算，有⼏个 j 能够使得 sum[i] 和 sum[j] 的差为 k。毎找到⼀个这样的 j ，就把结果加⼀。 我们可以把 if 语句⾥的条件判断移项，这样写：
if (sum[j] == sum[i] - k) 
    ans++;
//优化的思路是：我直接记录下有⼏个 sum[j] 和 sum[i] - k 相等，直接更 新结果，就避免了内层的 for 循环。
//我们可以⽤哈希表，在记录前缀和的同 时记录该前缀和出现的次数。
int subarraySum(int[] nums, int k) { 
    int n = nums.length; // map：前缀和 -> 该前缀和出现的次数 
    HashMap<Integer, Integer>;
    preSum = new HashMap<>(); 
    // base case 
    preSum.put(0, 1); 
    
    int ans = 0, sum0_i = 0; 
    for (int i = 0; i < n; i++) { 
        sum0_i += nums[i]; 
        // 这是我们想找的前缀和 nums[0..j] 
        int sum0_j = sum0_i - k; 
        // 如果前⾯有这个前缀和，则直接更新答案 
        if (preSum.containsKey(sum0_j)) 
            ans += preSum.get(sum0_j); 
        // 把前缀和 nums[0..i] 加⼊并记录出现次数 
        preSum.put(sum0_i, preSum.getOrDefault(sum0_i, 0) + 1); 
    }
    return ans; 
}

这样，就把时间复杂度降到了 O(N) ，是最优解法了。

总结

前缀和不难，却很有⽤，主要⽤于处理数组区间的问题。 ⽐如说，让你统计班上同学考试成绩在不同分数段的百分⽐，也可以利⽤前 缀和技巧

1
2
3
4
5
6
7
8
int[] scores; // 存储着所有同学的分数 
// 试卷满分 150 分 
int[] count = new int[150 + 1] // 记录每个分数有⼏个同学 
    for (int score : scores)
        count[score]++;
// 构造前缀和 
for (int i = 1; i < count.length; i++) 
    count[i] = count[i] + count[i-1];

这样，给你任何⼀个分数段，你都能通过前缀和相减快速计算出这个分数段 \的⼈数，百分⽐也就很容易计算了。

但是，稍微复杂⼀些的算法问题，不⽌考察简单的前缀和技巧。⽐如本⽂探 讨的这道题⽬，就需要借助前缀和的思路做进⼀步的优化，借助哈希表去除 不必要的嵌套循环。可⻅对题⽬的理解和细节的分析能⼒对于算法的优化是 ⾄关重要的。

发表于 更新于 分类于

jQuery基础

jQuery 是一个 JavaScript 库。jQuery 极大地简化了 JavaScript 编程。

jQuery库包含以下功能：

  • HTML 元素选取
  • HTML 元素操作
  • CSS 操作
  • HTML 事件函数
  • JavaScript 特效和动画
  • HTML DOM 遍历和修改
  • AJAX
  • Utilities

提示： 除此之外，Jquery还提供了大量的插件。

jQuery语法

jQuery 语法是通过选取 HTML 元素，并对选取的元素执行某些操作。

基础语法： $(*selector*).*action*()

  • 美元符号定义 jQuery
  • 选择符（selector）”查询”和”查找” HTML 元素
  • jQuery 的 action() 执行对元素的操作

实例:

  • $(this).hide() - 隐藏当前元素
  • $(“p”).hide() - 隐藏所有

    元素

  • $(“p.test”).hide() - 隐藏所有 class=”test” 的

    元素

  • $(“#test”).hide() - 隐藏 id=”test” 的元素
1
2
3
4
5
6
7
8
9
10
11
12
//在我们的实例中的所有 jQuery 函数位于一个 document ready 函数中：
$(document).ready(function(){
 
   // 开始写 jQuery 代码...
 
});
/*这是为了防止文档在完全加载（就绪）之前运行 jQuery 代码，即在 DOM 加载完成后才可以对 DOM 进行操作。

如果在文档没有完全加载之前就运行函数，操作可能失败。下面是两个具体的例子：

试图隐藏一个不存在的元素
获得未完全加载的图像的大小*/

jQuery选择器

jQuery 选择器允许您对 HTML 元素组或单个元素进行操作。jQuery 选择器基于元素的 id、类、类型、属性、属性值等”查找”（或选择）HTML 元素。 它基于已经存在的 CSS 选择器，除此之外，它还有一些自定义的选择器。

jQuery 中所有选择器都以美元符号开头：$()。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
//jQuery 元素选择器基于元素名选取元素,在页面中选取所有 <p> 元素。
//用户点击按钮后，所有 <p> 元素都隐藏。
$(document).ready(function(){
  $("button").click(function(){
    $("p").hide();
  });
});
//jQuery #id 选择器通过 HTML 元素的 id 属性选取指定的元素。
//页面中元素的 id 应该是唯一的，所以您要在页面中选取唯一的元素需要通过 #id 选择器。
$(document).ready(function(){
  $("button").click(function(){
    $("#test").hide();
  });
});
//jQuery 类选择器可以通过指定的 class 查找元素。
$(document).ready(function(){
  $("button").click(function(){
    $(".test").hide();
  });
});
//如果您的网站包含许多页面，并且您希望您的 jQuery 函数易于维护，那么请把您的 jQuery 函数放到独立的 .js 文件中。
//当我们在教程中演示 jQuery 时，会将函数直接添加到 <head> 部分中。不过，把它们放到一个单独的文件中会更好，就像这样（通过 src 属性来引用文件）：
<head>
<script src="http://cdn.static.runoob.com/libs/jquery/1.10.2/jquery.min.js">
</script>
<script src="my_jquery_functions.js"></script>
</head>

jQuery事件

在 jQuery 中，大多数 DOM 事件都有一个等效的 jQuery 方法。页面中指定一个点击事件：下一步是定义什么时间触发事件，可以通过一个事件函数来实现；

常用的 jQuery 事件方法

$(document).ready()

$(document).ready() 方法允许我们在文档完全加载完后执行函数。该事件方法在 jQuery 语法 章节中已经提到过。

click()

click() 方法是当按钮点击事件被触发时会调用一个函数。该函数在用户点击 HTML 元素时执行。

dblclick()

当双击元素时，会发生 dblclick 事件。

dblclick() 方法触发 dblclick 事件，或规定当发生 dblclick 事件时运行的函数：

mouseenter()

当鼠标指针穿过元素时，会发生 mouseenter 事件。

mouseenter() 方法触发 mouseenter 事件，或规定当发生 mouseenter 事件时运行的函数：

mouseleave()

当鼠标指针离开元素时，会发生 mouseleave 事件。

mouseleave() 方法触发 mouseleave 事件，或规定当发生 mouseleave 事件时运行的函数：

mousedown()

当鼠标指针移动到元素上方，并按下鼠标按键时，会发生 mousedown 事件。

mousedown() 方法触发 mousedown 事件，或规定当发生 mousedown 事件时运行的函数

mouseup()

当在元素上松开鼠标按钮时，会发生 mouseup 事件。

mouseup() 方法触发 mouseup 事件，或规定当发生 mouseup 事件时运行的函数：

hover()

hover()方法用于模拟光标悬停事件。

当鼠标移动到元素上时，会触发指定的第一个函数(mouseenter);当鼠标移出这个元素时，会触发指定的第二个函数(mouseleave)。

focus()

当元素获得焦点时，发生 focus 事件。

当通过鼠标点击选中元素或通过 tab 键定位到元素时，该元素就会获得焦点。

focus() 方法触发 focus 事件，或规定当发生 focus 事件时运行的函数

blur()

当元素失去焦点时，发生 blur 事件。

blur() 方法触发 blur 事件，或规定当发生 blur 事件时运行的函数：

jQuery效果

隐藏与显示

通过 jQuery，您可以使用 hide() 和 show() 方法来隐藏和显示 HTML 元素：

1
2
3
4
5
6
7
8
9
10
11
12
$(selector).hide(speed,callback);
$(selector).show(speed,callback);
//可选的 speed 参数规定隐藏/显示的速度，可以取以下值："slow"、"fast" 或毫秒。
//可选的 callback 参数是隐藏或显示完成后所执行的函数名称。

//通过 jQuery，您可以使用 toggle() 方法来切换 hide() 和 show() 方法。
//显示被隐藏的元素，并隐藏已显示的元素：
$("button").click(function(){
  $("p").toggle();
});
$(selector).toggle(speed,callback);
//可选的 speed 参数规定隐藏/显示的速度，可以取以下值："slow"、"fast" 或毫秒。可选的 callback 参数是隐藏或显示完成后所执行的函数名称。

淡入淡出

通过 jQuery，您可以实现元素的淡入淡出效果。jQuery 拥有下面四种 fade 方法：

  • fadeIn()
  • fadeOut()
  • fadeToggle()
  • fadeTo()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
//jQuery fadeIn() 用于淡入已隐藏的元素;
$(selector).fadeIn(speed,callback);
$("button").click(function(){
  $("#div1").fadeIn();
  $("#div2").fadeIn("slow");
  $("#div3").fadeIn(3000);
});

//jQuery fadeOut() 方法用于淡出可见元素
$(selector).fadeOut(speed,callback);
$("button").click(function(){
  $("#div1").fadeOut();
  $("#div2").fadeOut("slow");
  $("#div3").fadeOut(3000);
});

//jQuery fadeToggle() 方法可以在 fadeIn() 与 fadeOut() 方法之间进行切换。
//如果元素已淡出，则 fadeToggle() 会向元素添加淡入效果。如果元素已淡入，则 fadeToggle() 会向元素添加淡出效果。
$("button").click(function(){
  $("#div1").fadeToggle();
  $("#div2").fadeToggle("slow");
  $("#div3").fadeToggle(3000);
});

//jQuery fadeTo() 方法允许渐变为给定的不透明度（值介于 0 与 1 之间）。
$("button").click(function(){
  $("#div1").fadeTo("slow",0.15);
  $("#div2").fadeTo("slow",0.4);
  $("#div3").fadeTo("slow",0.7);
});

滑动效果

通过 jQuery，您可以在元素上创建滑动效果。jQuery 拥有以下滑动方法：

  • slideDown()
  • slideUp()
  • slideToggle()
1
2
3
4
//jQuery slideDown() 方法用于向下滑动元素。
//jQuery slideUp() 方法用于向上滑动元素。
//jQuery slideToggle() 方法可以在 slideDown() 与 slideUp() 方法之间进行切换。
//如果元素向下滑动，则 slideToggle() 可向上滑动它们。如果元素向上滑动，则 slideToggle() 可向下滑动它们。

jQuery动画

jQuery animate() 方法用于创建自定义动画。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
$(selector).animate({params},speed,callback);
/*必需的 params 参数定义形成动画的 CSS 属性。

可选的 speed 参数规定效果的时长。它可以取以下值："slow"、"fast" 或毫秒。

可选的 callback 参数是动画完成后所执行的函数名称。

下面的例子演示 animate() 方法的简单应用。它把 <div> 元素往右边移动了 250 像素：*/
$("button").click(function(){
  $("div").animate({left:'250px'});
});
//默认情况下，所有的 HTML 元素有一个静态的位置，且是不可移动的。 如果需要改变为，我们需要将元素的 position 属性设置为 relative, fixed, 或 absolute!

//同样生成动画的过程中可以同时使用多个属性
$("button").click(function(){
  $("div").animate({
    left:'250px',
    opacity:'0.5',
    height:'150px',
    width:'150px'
  });
});

//：当使用 animate() 时，必须使用 Camel 标记法书写所有的属性名，比如，必须使用 paddingLeft 而不是 padding-left，使用 marginRight 而不是 margin-right，等等。

//也可以定义相对值（该值相对于元素的当前值）。需要在值的前面加上 += 或 -=：
//默认地，jQuery 提供针对动画的队列功能。
//这意味着如果您在彼此之后编写多个 animate() 调用，jQuery 会创建包含这些方法调用的"内部"队列。然后逐一运行这些 animate 调用。
$("button").click(function(){
  var div=$("div");
  div.animate({left:'100px'},"slow");
  div.animate({fontSize:'3em'},"slow");
});

//

jQuery stop() 方法用于在动画或效果完成前对它们进行停止。stop() 方法适用于所有 jQuery 效果函数，包括滑动、淡入淡出和自定义动画

$(selector).stop(stopAll,goToEnd)。

可选的 stopAll 参数规定是否应该清除动画队列。默认是 false，即仅停止活动的动画，允许任何排入队列的动画向后执行。可选的 goToEnd 参数规定是否立即完成当前动画。默认是 false。因此，默认地，stop() 会清除在被选元素上指定的当前动画。

Callback 函数在当前动画 100% 完成之后执行。

jQuery链

通过 jQuery，可以把动作/方法链接在一起。Chaining 允许我们在一条语句中运行多个 jQuery 方法（在相同的元素上）

直到现在，我们都是一次写一条 jQuery 语句（一条接着另一条）。

不过，有一种名为链接（chaining）的技术，允许我们在相同的元素上运行多条 jQuery 命令，一条接着另一条。提示： 这样的话，浏览器就不必多次查找相同的元素。如需链接一个动作，您只需简单地把该动作追加到之前的动作上。下面的例子把 css()、slideUp() 和 slideDown() 链接在一起。”p1” 元素首先会变为红色，然后向上滑动，再然后向下滑动：

1
2
3
4
5
6
7
$("#p1").css("color","red").slideUp(2000).slideDown(2000);
//如果需要，我们也可以添加多个方法调用。
//提示：当进行链接时，代码行会变得很长。不过，jQuery 语法不是很严格；您可以按照希望的格式来写，包含换行和缩进。如下书写也可以很好地运行：
$("#p1").css("color","red")
  .slideUp(2000)
  .slideDown(2000);
//jQuery 会抛掉多余的空格，并当成一行长代码来执行上面的代码行。

什么是链式调用

链式调用完方法后，return this返回当前调用方法的对象。普通的定义类方法，在多次调用一个对象的不同方法时有一个弊端，就是会多次重复使用一个对象变量，进行了多次查找，可以在原本的实现类中增添一行return this 从而能简单地实现链式调用。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//创建一个bird类
    function Bird(name) {
        this.name=name;
        this.run=function () {
            document.write(name+" "+"start run;");
            return this;// return this返回当前调用方法的对象。
        }
        this.stopRun=function () {
            document.write(name+" "+"start run;");
            return this;
        }
        this.sing=function () {
            document.write(name+" "+"start sing;");
            return this;
        }
        this.stopSing=function () {
            document.write(name+" "+"start stopSing;");
            return this;
        }
    }


var bird=new Bird("测试");
    bird.run().sing().stopSing().stopRun();
//结果为;测试 start run;测试 start sing;测试 start stopSing;测试 start run;

jq的链式调用

jq的链式调用其实就是比如我们在选择dom的时候，

1
2
3
4
5
6
7
8
9
10
11
12
$('input[type="button"]')
    .eq(0).click(function() {
        alert('点击我!');
}).end().eq(1)
.click(function() {
    $('input[type="button"]:eq(0)').trigger('click');
}).end().eq(2)
.toggle(function() {
    $('.aa').hide('slow');
}, function() {
    $('.aa').show('slow');
});

比如如上代码，先选择type类型为button的所有DOM，然后再选择第一个…

我们自然想到每次其实就是返回选择后的结果，在js里面有什么东西可以指代这个吗？
如果你想到this就对了。

q的方法都是挂在原型的，那么如果我们每次在内部方法返回this，也就是返回实例对象，那么我们就可以继续调用原型上的方法了，这样的就节省代码量，提高代码的效率，代码看起来更优雅。

但是也会出现一个问题：所有对象的方法返回的都是对象本身，也就是说没有返回值，所以这种方法不一定在任何环境下都适合。

模仿jQuery的链式调用

1、定义一个含参数的空对象；

1
2
3
4
(function(){
  //下划线：表示私有变量的写法
    function _$(els) { };//有参数的空函数对象
})()//程序启动的时候 里面的代码直接执行了

2、准备方法：在_$上定义一个onrReady方法；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(function(){
   //第一步，下划线：表示私有变量的写法
    function _$(els) { };//有参数的空对象
    //第二步，准备方法  在_$上定义一个onrReady方法
    _$.onrReady=function (fn) {
        //按要求把对象（_$）注册到window对象上
        //对外开放的接口
        window.$=function () {
            return new _$(arguments);
            //传递相应的方法调用参数  返回一可以使用function类原型上的方法的对象（$("")=_$(参数)）
        }
        fn();
    }
    }
})()

3、为了类能扩展函数，我们定义一个它的静态函数

1
2
3
4
Function.prototype.method=function (name,fn) {//（函数名称，函数本身）
     this.prototype[name]=fn;
     return this;//链式调用关键
};//这个函数的意思：为function对象增加函数，会用链式调用，链式调用有两个参数name,和fn

4、扩展类的相应方法，链式的对象增加jquery库提供的操作函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
(function(){
    //下划线：表示私有变量的写法
    function _$(els) { };//有参数的空对象
    //第二步，准备方法  在_$上定义一个onrReady方法
    _$.onrReady=function (fn) {
        //按要求把对象（_$）注册到window对象上   
        //对外开放的接口
        window.$=function () {
            return new _$(arguments);//传递相应的方法调用参数  返回一可以使用function类原型上的方法的对象（$("")=_$(参数)）
        }
        fn();
    }
     //第四步
    //扩展类的相应方法  链式的对象增加jquery库提供的操作函数  
_$.method("AddEvent",function (type,fn) {//_$本身是一个function要继承原型链上的东西。
    fn();
}).method("getEvent",function (fn,e) {
    fn();
})
})()

5、使用，需要调用_$.onReady方法才可以返回对象使用从function类继承而来的原型上的方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
(function () {
    // （1）下划线：表示私有变量的写法
    function _$(els) { };//有参数的空对象
    //（2）准备方法  在_$上定义一个onrReady方法
      // window.$=_$;
    _$.onrReady=function (fn) {
        //按要求把对象（_$）注册到window对象上   在任何地方都可以使用
        //对外开放的接口
        window.$=function () {//window 上先注册一个全局变量 与外界产生关系
            return new _$(arguments);//传递相应的方法调用参数  返回一可以使用function类原型上的方法的对象（$("")=_$(参数)）
        }
        fn();
    }
    //（4）扩展类的相应方法  链式的对象增加jquery库提供的操作函数
_$.method("AddEvent",function (type,fn) {//_$本身是一个function要继承原型链上的东西。
    fn();
}).method("getEvent",function (fn,e) {
    fn();
});
    //第五步，开始使用 ，需要调用_$.onready方法才可以返回对象使用从function类继承而来的原型上的方法
     _$.onrReady(function () {//$是绑定在Windows上的
        $("").AddEvent("click",function () {
            alert("click")
        })
    })
})()

链式调用

简单的加减法链式调用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(function(){
    function test(Number){
        return isNaN(Number)?Number:0
    }
    function Add(num){
        test(num)
        return this + num
    }
      function jian(num){
           test(num)
        return this - num
    }
    Function.prototype.Add = Add
    Function.prototype.jian = jian

})()